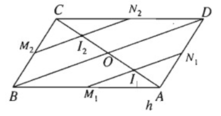
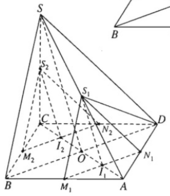
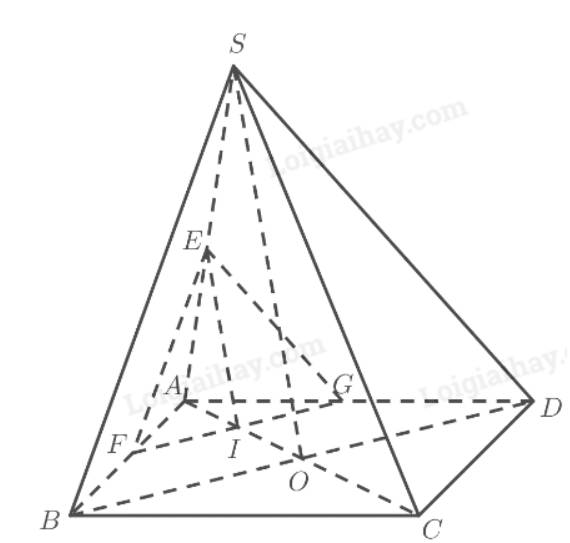
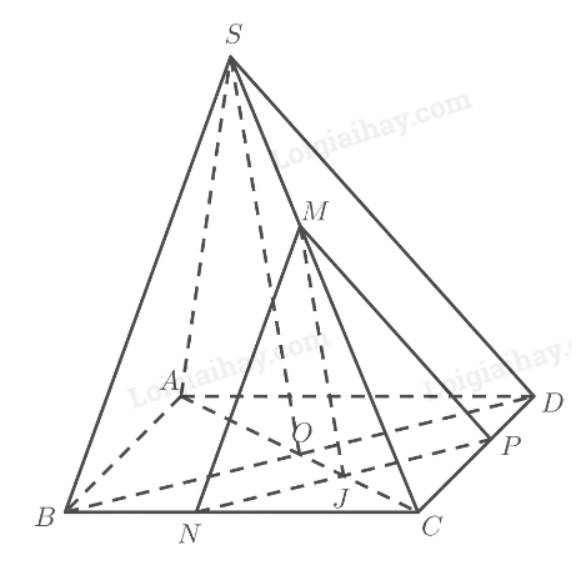
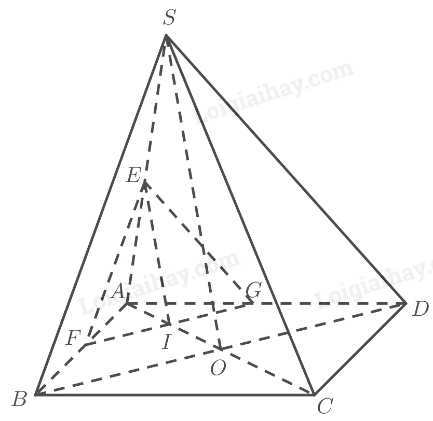
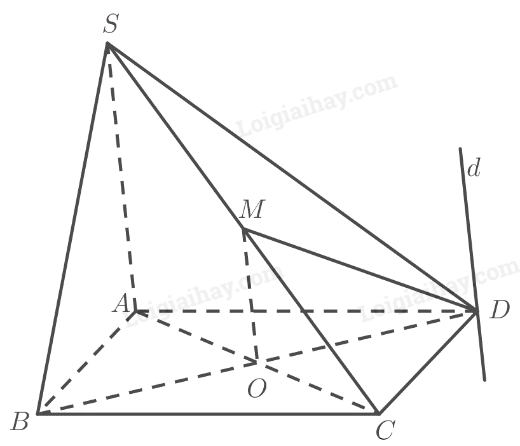
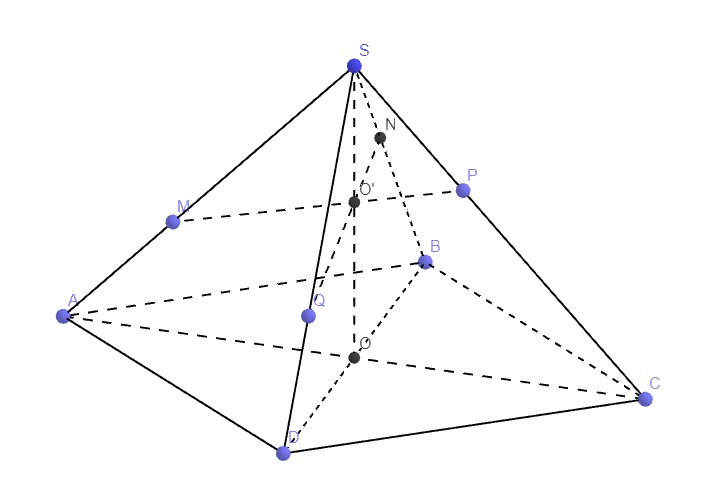
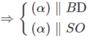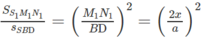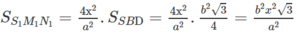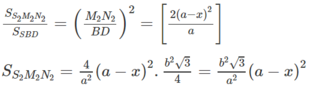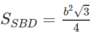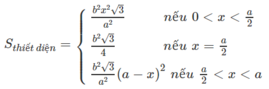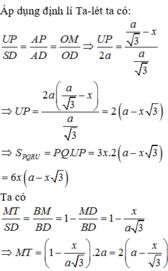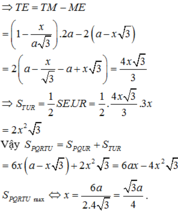Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với \(AI=x,\left(0< x< a\right)\). Lấy \(\left(\alpha\right)\) là mặt phẳng đi qua I và song song với mặt phẳng (SBD)
a) Xác định thiết diện của mặt phẳng \(\left(\alpha\right)\) với hình chóp S.ABCD
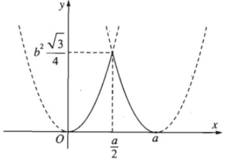
b) Tìm diện tích S của thiết diện ở câu a) theo \(a,b,x\). Tìm \(x\) để S lớn nhất ?