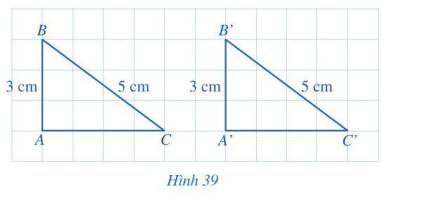
Cho tam giác vuông ABC ( \(\widehat{A}=90^0\)), AB = 21 cm, AC = 28 cm; đường phân giác góc A cắt BC tại D, đường thẳng qua D và song song với AB, cắt AC tại E (h.18)
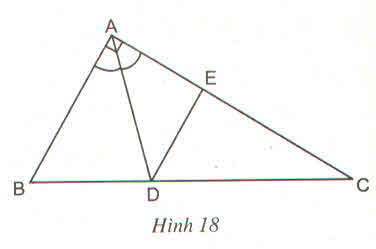
a) Tính độ dài các đoạn thẳng BD, DC và DE
b) Tính diện tích tam giác ABD và diện tích tam giác ACD