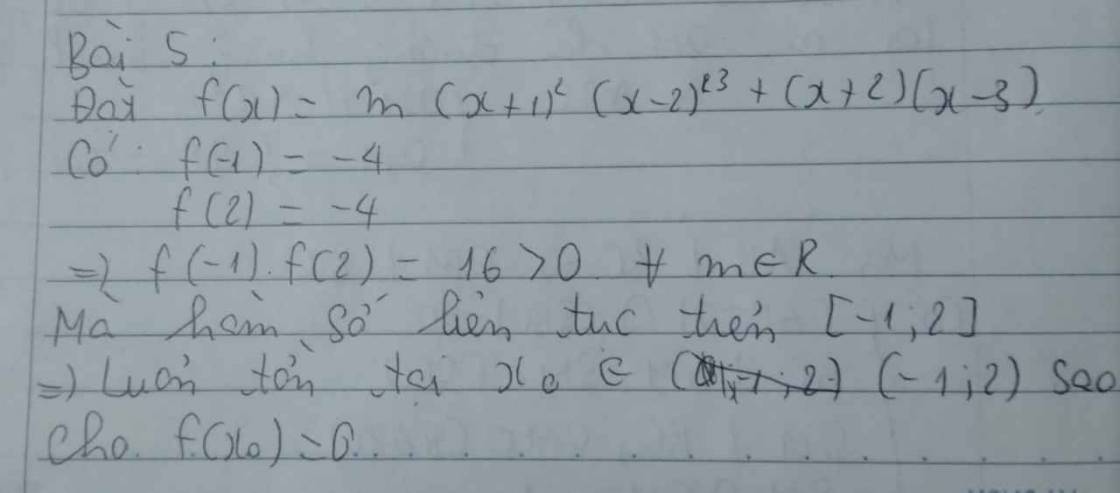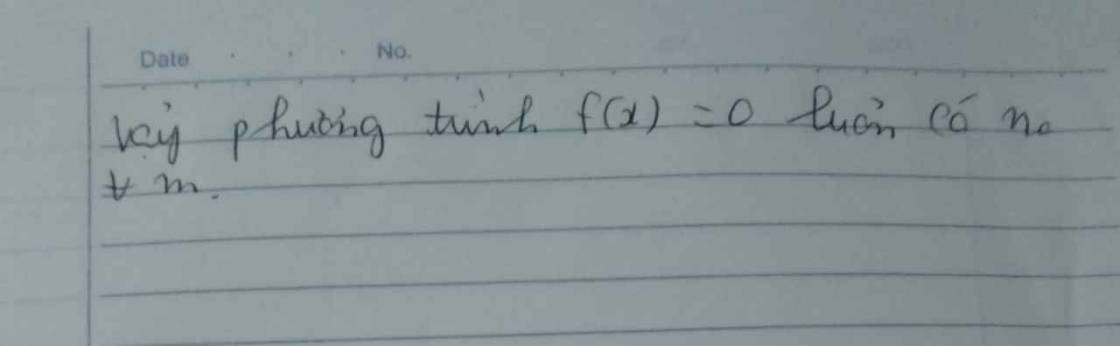1.

Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)

\(f\left(x\right)\) xác định và liên tục trên R

\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)

\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)

\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)

\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)

\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)

\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)

\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)

\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)

Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt

2.

Đặt \(t=g\left(x\right)=x.cosx\)

\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)

\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)

Hàm \(f\left(t\right)\) xác định và liên tục trên R

\(f\left(1\right)=1>0\)

\(f\left(-2\right)=-8< 0\)

\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m

3. Chắc ngoặc thứ là \(\left(2m^2-2m+4040\right)\) ?

\(\Leftrightarrow\left(m^2-m+2021\right)x^3-2\left(m^2-m+2020\right)x^2-4x+m^2-m+2021=0\)

Do \(m^2-m+2020>0\), đặt \(m^2-m+2020=n^2\)

\(\Rightarrow\left(n^2+1\right)x^3-2n^2x^2-4x+n^2+1=0\)

Quy về bài số 1

Xét hàm số f(x)=m(x+1)2(x−2)3+(x+2)(x−3)f(x)=m(x+1)2(x−2)3+(x+2)(x−3) xác định và liên tục trên RR

⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].

Ta có: {f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2{f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2.

+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0

⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.

+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0

⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).

Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.

Xét hàm số \(f\left(x\right)=m\left(x+1\right)^2\left(x-2\right)^3+\left(x+2\right)\left(x-3\right)\)
f(x)=m(x+1)2(x−2)3+(x+2)(x−3), \(D=ℝ\)
R⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].

Ta có: \(\left\{{}\begin{matrix}f\left(-2\right)=-64m\\f\left(3\right)=16m\end{matrix}\right.\)
\(\Rightarrow f\left(-2\right).f\left(3\right)=-1024m^2\)

+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0

⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.

+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0

⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).

Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.

Xét hàm \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)

Hàm \(f\left(x\right)\) là hàm liên tục trên R

\(f\left(1\right)=-2< 0\)

\(f\left(-2\right)=13>0\)

\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(f\left(2\right)=13>0\Rightarrow f\left(1\right).f\left(2\right)< 0\)

\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\)

\(\Rightarrow\) Phương trình đã cho luôn có ít nhất 2 nghiệm với mọi m

\(f\left(x\right)=\left(1-m^2\right)\left(x+1\right)^3+x^2-x-3\) là hàm đa thức liên tục trên R. Do đó nó liên tục trên \(\left[-2;-1\right]\)

Ta có \(f\left(-1\right)=-1< 0\) và \(f\left(-2\right)=m^2+2>0\) nên \(f\left(-1\right)f\left(-2\right)< 0\) với mọi m.

Do đó, phương trình \(f\left(x\right)=0\) luôn có ít nhất một nghiệm trong khoảng (-2; -1) với mọi m. Nghĩa là, phương trình \(\left(1-m^2\right)\left(x+1\right)^3+x^2-x-3=0\) luôn có nghiệm với mọi m.

Xét pt cho là pt bậc hai một ẩn $x$ ( Với $a=1 \neq 0, b=-2(m-1), c = m-3$ )

Ta có : \(\Delta'=b'^2-ac\)

\(=\left[-\left(m-1\right)\right]^2-\left(m-3\right)\cdot1\)

\(=m^2-2m+1-m+3\)

\(=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\)

Nên pt cho luôn có hai nghiệm phân biệt \(\forall m\)

Lời giải:

a.

Từ $x+y=2\Rightarrow y=2-x$. Thay vào PT(2):
$(m+1)x+m(2-x)=7$

$\Leftrightarrow x+2m=7$

$\Leftrightarrow x=7-2m$

$y=2-x=2-(7-2m)=2m-5$

Vậy hpt có nghiệm $(x,y)=(7-2m, 2m-5)(*)$

Nếu $x,y$ có 1 số $\geq 0$, một số $\leq 0$ thì $xy\leq 0< 1$

Nếu $x,y$ cùng $\geq 0$ thì áp dụng BĐT Cô-si:

$2=x+y\geq 2\sqrt{xy}\Rightarrow xy\leq 1$

Vậy tóm lại $xy\leq 1(**)$
Từ $(*); (**)$ suy ra với mọi $m$ thì hpt luôn có nghiệm $x,y$ thỏa mãn $xy\leq 1$

b.

$xy>0$

$\Leftrightarrow (7-2m)(2m-5)>0$

$\Leftrightarrow 7> 2m> 5$

$\Leftrightarrow \frac{7}{2}> m> \frac{5}{2}$

Do $m$ nguyên nên $m=3$

Thử lại thấy đúng.

x ≤ 0 ⇒ |x| = -x

Suy ra: x + |x| = x – x = 0

Vậy mọi x ≤ 0 đều là nghiệm của phương trình x + |x| = 0

a=-1; b=-2m^2-2m-2; c=m^2+m+1

A=a*c=-(m^2+m+1)

=-(m^2+m+1/4+3/4)

=-(m+1/2)^2-3/4<0

=>Phương trình luôn có hai nghiệm phân biệt

a, - Xét phương trình (1) có : \(\Delta^,=b^{,2}-ac\)

\(=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5\)

\(=m^2-4m+6=m^2-4m+4+2=\left(m-2\right)^2+2\)

- Thấy \(\Delta^,\ge2>0\) => ĐPCM .

b,Theo viets : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)

\(TH_1:x_1=0\Rightarrow m=\dfrac{5}{2}\)

- Thay m và x1 vào một PT ta được : x2 = -3 ( L )

=> Không tồn tại x1 = 0 để nghiệm còn lại lớn hơn 0 .

\(TH_2:x_1< 0< x_2\)

\(\Leftrightarrow ac< 0\)

\(\Leftrightarrow m< \dfrac{5}{2}\)

Vậy ...