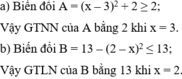+) \(A=\left(x-3\right)^2+2\)

Vì \(\left(x-3\right)^2\)≥0 ∀x

⇒\(A\)≥2 ∀x

Min A=2⇔\(x=3\)

+) \(B=11-x^2\)

Câu này chỉ tìm được max thôi nha

\(A=\left(x-3\right)^2+2\)

Vì \(\left(x-3\right)^2\ge0\)

\(\Rightarrow\left(x-3\right)^2+2\ge2\)

Vậy GTNN của A là 2 khi x = 3

A = x² - 7x + 11

<=> A = x² - 7x + (3,5)² - 1,25

<=> A = (x - 3,5)² - 1,25

Do: (x - 3,5)² lớn hơn hoặc = 0

=> A lớn hơn hoặc bằng -1,25

Dấu "=" xảy ra khi: (x - 3,5)² = 0   <=> x = 3,5

Vậy x = 3,5

1: Ta có: \(x^2-2x-5\)

\(=x^2-2x+1-6\)

\(=\left(x-1\right)^2-6\ge-6\forall x\)

Dấu '=' xảy ra khi x=1

2: ta có: \(3x^2+5x-2\)

\(=3\left(x^2+\dfrac{5}{3}x-\dfrac{2}{3}\right)\)

\(=3\left(x^2+2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}-\dfrac{49}{36}\right)\)

\(=3\left(x+\dfrac{5}{6}\right)^2-\dfrac{49}{12}\ge-\dfrac{49}{12}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{5}{6}\)

Ta có: A =  x 2 - 6 x + 11  =  x 2 - 2 . 3 x + 9 + 2  = x - 3 2 + 2

Vì x - 3 2  ≥ 0 nên  x - 3 2  + 2 ≥ 2

Suy ra: A ≥ 2.

A = 2 khi và chỉ khi x - 3 = 0 suy ra x = 3

Vậy A = 2 là giá trị nhỏ nhất của biểu thức tại x =3.

Ta có: x^2-7x+11

=x^2-7x+12,25-1,25

=x^2-2.3,5x+3,5^2-1,25

=(x-3,5)^5-1,25

Ma: (x-3,5)^2\(\ge\)0

\(\Rightarrow\)(x-3,5)^2-1,25 \(\ge\)-1,25

Vậy Min của A là: -1,25

Dấu "=" xảy ra khi: x-3,5=0 \(\Rightarrow\) x=3,5

<=> A = x² - 7x + (3,5)² - 1,25

<=> A = (x - 3,5)² - 1,25

Do: (x - 3,5)² \(\ge\)0   <=> A \(\ge\)-1,25

Dấu "=" xảy ra khi và chỉ khi: (x - 3,5)² = 0   <=> x = 3,5

Vậy MinA = -1,25 khi và chỉ khi x = 3,5

ta có A = x²-7x+11

A = x²-7x+12,25-1,25=(x-3,5)²-1,25>=-1,25 với mọi x

dấu bằng xảy ra khi x-3,5=0

                                 x=3,5

vậy GTNN của A = -1,25 khi x=3,5

`A=x^2-4x+1`
`=x^2-4x+4-3`
`=(x-2)^2-3>=-3`
Dấu "=" xảy ra khi x=2
`B=4x^2+4x+11`
`=4x^2+4x+1+10`
`=(2x+1)^2+10>=10`
Dấu "=" xảy ra khi `x=-1/2`
`C=(x-1)(x+3)(x+2)(x+6)`
`=[(x-1)(x+6)][(x+3)(x+2)]`
`=(x^2+5x-6)(x^2+5x+6)`
`=(x^2+5x)^2-36>=-36`
Dấu "=" xảy ra khi `x=0\or\x=-5`
`D=5-8x-x^2`
`=21-16-8x-x^2`
`=21-(x^2+8x+16)`
`=21-(x+4)^2<=21`
Dấu "=" xảy ra khi `x=-4`
`E=4x-x^2+1`
`=5-4+4-x^2`
`=5-(x^2-4x+4)`
`=5-(x-2)^2<=5`
Dấu "=" xảy ra khi `x=5`

A= x² - 4x +1

   = x² - 4x + 4 - 3

   = (x-2)² -3

Ta có (x-2)² ≥ 0 ∀ x

    ⇒ (x-2)² -3 ≥ -3 ∀ x

Vậy A_Min= -3 tại x=2

B= 4x²+4x+11

  = 4x²+4x+1+10

  = (2x+1)²+10

Ta có (2x+1)² ≥ 0 ∀ x

     ⇒ (2x+1)²+10 ≥ 10 ∀ x

Vậy B_Min=10 tại x= \(\dfrac{-1}{2}\)

C=(x-1)(x+3)(x+2)(x+6)

  = (x-1)(x+6)(x+3)(x+2)

  = (x²+5x-6) (x²+5x+6)

  = (x²+5x)² -36

Ta có (x²+5x)² ≥ 0 ∀ x
  ⇒ (x²+5x)² -36 ≥ -36 ∀ x

Vậy C_Min=-36 tại x=0 hoặc x= -5

\(\Delta=4m^2+69\ge0\Leftrightarrow\begin{matrix}m\ge\dfrac{\sqrt{69}}{2}\\m\le-\dfrac{\sqrt{69}}{2}\end{matrix}\)

viet : \(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=-\left(m^2+5\right)\end{matrix}\right.\)

ta có : \(A=\left(x_1+x_2\right)^2-x_1x_2+2m=49+m^2+5+2m=m^2+2m+54\)

vì \(m\ge\dfrac{\sqrt{69}}{2}\Rightarrow m^2+2m+54\ge\dfrac{69+2\sqrt{69}+216}{4}\) hay \(A\ge\dfrac{69+2\sqrt{69}+216}{4}\)

\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)

b:

\(D=-25x^2+10x-1-10\)

\(=-\left(25x^2-10x+1\right)-10\)

\(=-\left(5x-1\right)^2-10< =-10\)

Dấu = xảy ra khi x=1/5

\(E=-9x^2-6x-1+20\)

\(=-\left(9x^2+6x+1\right)+20\)

\(=-\left(3x+1\right)^2+20< =20\)

Dấu = xảy ra khi x=-1/3

\(F=-x^2+2x-1+1\)

\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)

Dấu = xảy ra khi x=1

Bài 6:

a) Ta có: \(A=-x^2+6x-11\)

\(=-\left(x^2-6x+11\right)\)

\(=-\left(x-3\right)^2-2\le-2\forall x\)

Dấu '=' xảy ra khi x=3

b) Ta có: \(B=-x^2-8x+5\)

\(=-\left(x^2+8x-5\right)\)

\(=-\left(x^2+8x+16-21\right)\)

\(=-\left(x+4\right)^2+21\le21\forall x\)

Dấu '=' xảy ra khi x=-4

c) Ta có: \(C=-x^2+4x+1\)

\(=-\left(x^2-4x-1\right)\)

\(=-\left(x^2-4x+4-5\right)\)

\(=-\left(x-2\right)^2+5\le5\forall x\)

Dấu '=' xảy ra khi x=2

Bài 7:

a) Ta có: \(x^2-6x+11\)

\(=x^2-6x+9+2\)

\(=\left(x-3\right)^2+2\ge2\forall x\)

Dấu '=' xảy ra khi x=3