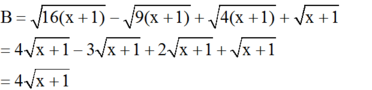\(a.\)

\(\dfrac{16x^2-1}{16x^2-8x+1}\\ =\dfrac{\left(4x\right)^2-1}{\left(4x-1\right)^2}\\ =\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\\ =\dfrac{4x+1}{4x-1}\)

\(b.\)

\(\dfrac{4x^2-4xy+y^2}{-\left(4x^2-y^2\right)}\\ =-\dfrac{\left(2x-y\right)^2}{\left(2x-y\right)\left(2x+y\right)}\\ =\dfrac{-\left(2x-y\right)}{2x+y}\\ =\dfrac{y-2x}{y+2x}\)

a) Ta có: \(\dfrac{16x^2-1}{16x^2-8x+1}\)

\(=\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\)

\(=\dfrac{4x+1}{4x-1}\)

b) Ta có: \(\dfrac{4x^2-4xy+y^2}{y^2-4x^2}\)

\(=\dfrac{\left(2x-y\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)

\(=\dfrac{\left(y-2x\right)^2}{\left(y-2x\right)\left(y+2x\right)}\)

\(=\dfrac{y-2x}{y+2x}\)

a) Pt \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=5\Leftrightarrow\left|x-2\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

Vậy...

b)Đk: \(x\ge-1\)

Pt \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}=16-\sqrt{x+1}\)

\(\Leftrightarrow4\sqrt{x+1}=16\)\(\Leftrightarrow x+1=16\)\(\Leftrightarrow x=15\) (tm)

Vậy...

\(A=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\) (a>0)

\(=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)

\(=a+\sqrt{a}-\left(2\sqrt{a}+1\right)+1=a-\sqrt{a}\)

b) \(A=a-\sqrt{a}=a-2.\dfrac{1}{2}\sqrt{a}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

Dấu "=" xảy ra khi \(\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\left(tmđk\right)\) 

Vậy \(A_{min}=-\dfrac{1}{4}\)

a) \(\sqrt{x^2-4x+4}=5\Rightarrow\sqrt{\left(x-2\right)^2}=5\Rightarrow\left|x-2\right|=5\)

\(\Rightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

b) \(\sqrt{16x+16}-3\sqrt{x+1}+\sqrt{4x+4}=16-\sqrt{x+1}\)

\(\Rightarrow\sqrt{16\left(x+1\right)}-3\sqrt{x+1}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}=16\)

\(\Rightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)

\(\Rightarrow4\sqrt{x+1}=16\Rightarrow\sqrt{x+1}=4\Rightarrow x=15\)

a) \(A=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\)

\(=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)

\(=a+\sqrt{a}-2\sqrt{a}-1+1=a-\sqrt{a}\)

b) Ta có: \(a-\sqrt{a}=\left(\sqrt{a}\right)^2-2.\sqrt{a}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)

\(=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

\(\Rightarrow A_{min}=-\dfrac{1}{4}\) khi \(a=\dfrac{1}{4}\)

✱ giải pt:

a.\(\sqrt{x^2-4x+4}\)\(=5\)

⇔\(\sqrt{\left(x-2\right)^2}=5\)

⇒\(\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

vậy....

b.\(\sqrt{16x+16}-3\sqrt{x+1}+\sqrt{4x+4}=16-\sqrt{x+1}\)

⇔ \(4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)

⇔ \(4\sqrt{x+1}=16\)

⇔ \(\sqrt{x+1}=16\)

⇒ \(x+1=256\)

⇔ \(x=255\)

vậy.....

a) x ≠ -5.

b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5  

c) Ta có P = 1 Û x = -4 (TMĐK)

d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .

Giúp với

Bài 1 : 

a, \(\left(x+3\right)^2+\left(x-3\right)^2+2\left(x^2-9\right)\)

\(=x^2+6x+9+x^2-6x+9+2x^2-18\)

\(=4x^2\)

b, \(\left(4x-1\right)^3-\left(4x-3\right)\left(16x^2+3\right)\)

\(=64x^3-32x^2+4x-16x^2+8x-1-64x^3-12x+48x^2+9=8\)

Bài 2 : 

a, \(16x-8xy+xy^2=x\left(16-8y+y^2\right)=x\left(4-y\right)^2\)

b, \(3\left(3-x\right)-2x\left(x-3\right)=3\left(3-x\right)+2x\left(3-x\right)=\left(3+2x\right)\left(3-x\right)\)

c, \(3x^2+4x-4=3x^2+6x-2x-4=\left(x+2\right)\left(3x-2\right)\)

Rút gọn biểu thức

a) ( x + 3 )²  + ( x - 3 )² + 2( x² - 9 )

= x³ + 6x + 9 + x² - 6x + 9 + 2x² - 18

= 4x²

b) ( 4x - 1 )³ - ( 4x - 3 )( 16x² + 3 )

= 64x³ - 48x² + 12x - 1 - ( 64x³ - 48x² + 12x - 9 )

= 64x³ - 48x² + 12x - 1 - 64x³ + 48x² - 12x + 9

= 8

PTĐTTNT

a) 16x - 8xy + xy²

= x( 16 - 8y + y² )

= x( 4 - y )²

b) 3( 3 - x ) ± 2x( x - 3 ) < không biết thay dấu gì (: >

= 3( 3 - x ) \(\mp\)2x( 3 - x )

= ( 3 - x )( 3 \(\mp\)2x ) 

c) 3x² + 4x - 4

= 3x² + 6x - 2x - 4

= 3x( x + 2 ) - 2( x + 2 )

= ( x + 2 )( 3x - 2 )

Tìm x

a) ( 3x - 2 )( 3x + 4 ) - ( 2 - 3x )² = 6

<=> ( 3x - 2 )( 3x + 4 ) - ( 3x - 2 )² = 6

<=> ( 3x - 2 )( 3x + 4 - 3x + 2 ) = 6

<=> ( 3x - 2 ).6 = 6

<=> 3x - 2 = 1

<=> x = 1

b) 2( x - 3 ) - ( x - 3 )( 3x - 2 ) = 0

<=> ( x - 3 )( 2 - 3x + 2 ) = 0

<=> ( x - 3 )( 4 - 3x ) = 0

<=> \(\orbr{\begin{cases}x-3=0\\4-3x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{4}{3}\end{cases}}\)

c) ( x - 1 )( x + 2 ) - x( x - 2 ) = -5

<=> x² + x - 2 - x² + 2x = -5

<=> 3x - 2 = -5

<=> 3x = -3

<=> x = -1

a) \(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)

b) \(=\dfrac{2y}{3\left(x+y\right)^2}=\dfrac{2y}{3x^2+6xy+3y^2}\)

c) \(=\dfrac{2x\left(x+1\right)}{x+1}=2x\)

d) \(=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}=\dfrac{x-y}{x+y}\)

e) \(=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}=-9\left(x-2\right)^2=-9x^2+36x-36\)

\(=\frac{x\left(16x^2-25\right)}{\left(x-3\right)\left(3-8+4x\right)}\)

\(=\frac{x\left(4x-5\right)\left(4x+5\right)}{\left(x-3\right)\left(4x-5\right)}\)

\(\frac{x\left(4x+5\right)}{x-3}=\)\(\frac{4x^2-5x}{x-3}\)

Rút gọn: