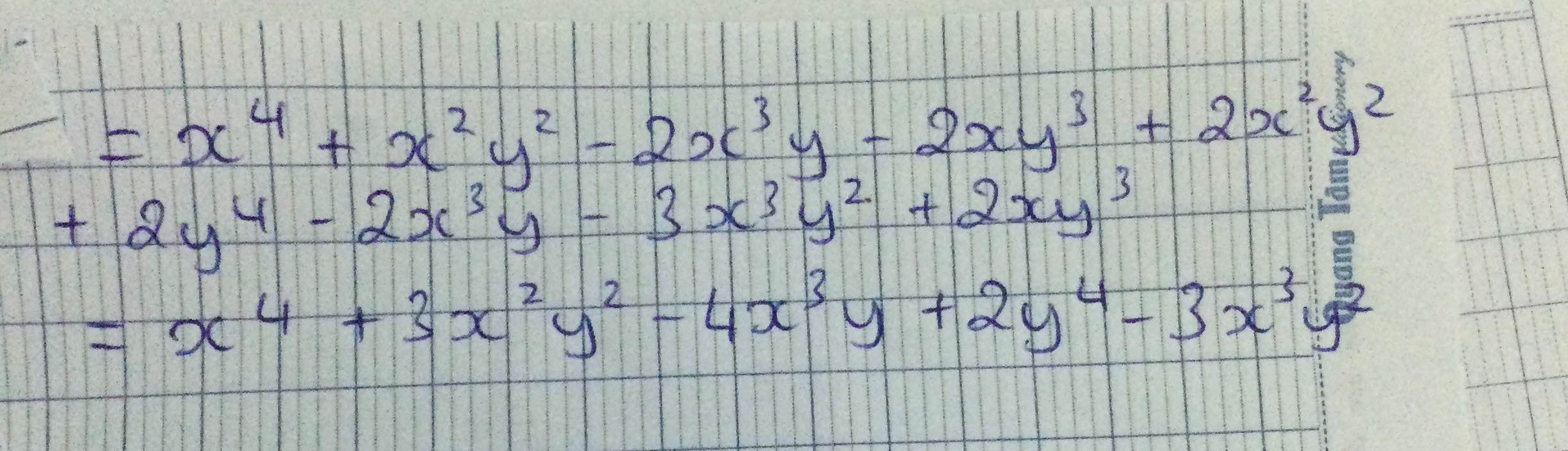\(2x^6+y^2-2x^3y=320\)

\(\Leftrightarrow x^6+\left(x^6-2x^3y+y^2\right)=320\)

\(\Leftrightarrow x^6+\left(x^3-y\right)^2=320\)

\(\Rightarrow x^6\le320\)

Mà\(x\in Z\)

\(\Rightarrow x^6=64;1;0\)

Xét từng trường hợp, bạn tìm ra được\(x^6=64\)thõa mãn

\(\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}}\)

+ x=2

=>y=-8;24

+x=-2

=>y=8;-24

Vậy\(\left(x;y\right)=\left(2;-8\right);\left(2;24\right);\left(-2;8\right);\left(-2;-24\right)\)

\(2x^6+y^2-2x^3y=320\)  \(\Leftrightarrow x^6+\left(x^6-2x^3y+y^2\right)=320\)\(\Leftrightarrow\) \(\left(x^3\right)^2+\left(x^3-y\right)^2=320\)

Vì \(\left(x^3\right)^2\ge0\)và  \(\left(x^3-y\right)^2\ge0\). Đồng thời \(\left(x^3\right)^2\)và  \(\left(x^3-y\right)^2\)cũng là hai số chính phương nên :

(  phân tích 320 thành tổng của 2 số chính phương ) 

\(\left(x^3\right)^2+\left(x^3-y\right)^2=8^2+16^2\) ( Do \(\sqrt[3]{16}\)không là 1 số nguyên nên \(x^3=8\))

Vậy ta có 4 trường hợp : 

+) Trường hợp 1: 

\(\hept{\begin{cases}\left(x^3\right)^2=8^2\\\left(x^3-y\right)^2=16^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x^3=8\\x^3-y=16\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=-8\end{cases}}}\)( TM )

+) Trường hợp 2:

\(\hept{\begin{cases}x^3=8\\x^3-y=-16\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=24\end{cases}}\left(TM\right)}\)

+) Trường hợp 3:

\(\hept{\begin{cases}x^3=-8\\x^3-y=16\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\y=-24\end{cases}\left(TM\right)}}\)

+) Trường hợp 4 :

\(\hept{\begin{cases}x^3=-8\\x^3-y=-16\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\y=8\end{cases}\left(TM\right)}}\)

Vậy phương trình có 4 cặp nghiệm (x;y) nguyên là (-2;8)  ,   (-2;-24 )   ,   (2;-8)    ;   ( 2; 24 )

ta có: \(2x^6+y^2-2x^3y=320\)

\(\Rightarrow\left(x^3-y\right)^2=320-x^6\)

mà \(\left(x^3-y\right)^2\ge0\)

nên \(320-x^6\ge0\Rightarrow x^6\le320\)

=>\(x^6\in\left\{0;1;64\right\}\)

với \(x^6=0\Rightarrow x=0\Rightarrow y^2=320\) loại vì 320 ko phải là số chính  phương

với \(x^6=1\Rightarrow\orbr{\begin{cases}x=1\\x=-1\end{cases}\Rightarrow\orbr{\begin{cases}\left(1-y\right)^2=319\\\left(-1-y\right)^2=319\end{cases}}}\)

loại vì 319  ko phải là số chính phương

với \(x^6=64\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}\Rightarrow\orbr{\begin{cases}\left(8-y\right)^2=256\\\left(-8-y\right)^2=256\end{cases}}}\)

khi \(\left(8-y\right)^2=256\Rightarrow\orbr{\begin{cases}8-y=16\\8-y=-16\end{cases}\Rightarrow\orbr{\begin{cases}y=-8\\y=24\end{cases}}}\)

khi \(\left(-8-y\right)^2=256\Rightarrow\orbr{\begin{cases}-8-y=16\\-8-y=-16\end{cases}\Rightarrow\orbr{\begin{cases}y=-24\\y=8\end{cases}}}\)

Vậy nghiệm của pt là : (x;y)={ (2;-8);(2;24);(-2;-24);(-2;8)}

PT <=> \(\left(y+2\right)x^2=y^2-1\)

- Nếu y = -2 <=> \(\left(-2\right)^2-1=0\) (vô lí)

=> \(y\ne-2\)

PT <=> \(x^2=\dfrac{y^2-1}{y+2}\)

Có \(x\in Z\Rightarrow x^2\in Z\)

=> \(\dfrac{y^2-1}{y+2}\in Z\)

=> \(y^2-1⋮y+2\)

=> \(y\left(y+2\right)-2\left(y+2\right)+3⋮y+2\)

=> \(3⋮y+2\)

Ta có bảng

KL: Vậy phương trình có tập nghiệm\(\left(x;y\right)=\left\{\left(0;1\right);\left(0;-1\right)\right\}\)

Ta có x⁴ + x² + 1 = y²

Lại có x⁴ + 2x² + 1 ≥ x⁴ + x² + 1 hay (x² + 1)² ≥ x⁴ + x² + 1

=> (x² + 1)² ≥ y² (1)

Lại có x⁴ + x² + 1 > x⁴ => y² > x⁴ (2)

Từ (1) và (2), ta có x⁴ < y² ≤ (x² + 1)²

<=> y² = (x² + 1)² = x⁴ + 2x² + 1

Mà x⁴ + x² + 1 = y² => x⁴ + 2x² + 1 = x⁴ + x² + 1

<=> x² = 0 <=> x = 0

Thay vào, ta có 1 = y² <=> y ∈ {-1,1}

Vậy ...

\(C=\left(x^2-2xy+y^2\right)\left(x^2+y^2\right)-2x^3y-3x^3y^2+2xy^3\)

\(=\left(x^2+y^2\right)^2-2xy\left(x^2+y^2\right)-xy\left(2x^2+3x^2y+2y^2\right)\)

\(=\left(x^2+y^2\right)^2-xy\left(2x^2+2y^2+2x^2+3x^2y+2y^2\right)\)

\(=\left(x^2+y^2\right)^2-xy\left(4x^2+3x^2y+4y^2\right)\)

Lời giải:

Hiển nhiên $x\geq 0$

Ta có: $2^x=y^2-57\equiv y^2\equiv 0,1\pmod 3$

$\Leftrightarrow (-1)^x\equiv 0,1\pmod 3$

$\Rightarrow x$ chẵn.

Đặt $x=2a$ với $a$ là số tự nhiên.

Khi đó: $2^{2a}-y^2=-57$

$\Leftrightarrow (2^a-y)(2^a+y)=-57$

Đến đây là dạng phương trình tích cực kỳ đơn giản nên bạn có thể tự xét TH để giải. Kết quả $a=3; y=11$ hay $x=6; y=7$

Lời giải:

Hiển nhiên $x\geq 0$

Ta có: $2^x=y^2-57\equiv y^2\equiv 0,1\pmod 3$

$\Leftrightarrow (-1)^x\equiv 0,1\pmod 3$

$\Rightarrow x$ chẵn.

Đặt $x=2a$ với $a$ là số tự nhiên.

Khi đó: $2^{2a}-y^2=-57$

$\Leftrightarrow (2^a-y)(2^a+y)=-57$

Đến đây là dạng phương trình tích cực kỳ đơn giản nên bạn có thể tự xét TH để giải. Kết quả $a=3; y=11$ hay $x=6; y=7$

<=>x^2+y^2-x-y-xy=0 
<=>2x^2+2y^2-2x-2y-2xy=0 
<=>(x-y)^2+(x-1)^2+(y-1)^2=2 
mà 2=0+1+1=1+0+1=1+1+0 
(phần này tách số 2 ra thành tổng 3 số chính phương) 
Xét trường hợp 1: 
(x-y)^2=0 
(x-1)^2=1 
(y-1)^2=1 
Giải ra ta được x=2, y=2 
Tương tự xét các trường hợp còn lại. 
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1) 

x² - xy + y² = x - y

<=> x² - xy + y² - x + y = 0

<=> x ( x - y) + y² - ( x - y) = 0

<=> (x-1)(x-y)y² =0

^{+4xy vào mỗi vế
=> nhóm VP = (xy+2)^2; VT = (2x+y)^2 + 3x + 3y
=> VT là SCP 
kẹp:}
(2x+y)^2< (2x+y)^2 + 3x + 3y<(2x+y+2)^2(do x,y nguyên dương)
=> (2x+y)^2 + 3x + 3y = (2x+y+1)^2
=> y = x+1 
thay vào 

x²y²+4=4x²+y²+3x+3y

tự làm nốt