GIÚ MÌN:
CHO DÃY 1;4;7;10;13;...
NẾU TA VIẾT LIỀN CÁC CHỮ SỐ NÀY LẠI THÀNH 1 SỐ THÌ CHỮ SỐ THỨ 302 CỦA SỐ TẠO THÀNH LÀ SỐ MẤY?
D = 1+3+32+33+34+....+32022
tính giá trị biểu thức giú tui với
![]()
\(D=1+3+3^2+3^3+3^4+...+3^{2022}\)
\(3D=3.\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(3D=3+3^2+3^3+3^4+3^5+...+3^{2023}\)
\(3D-D=\left(3+3^2+3^3+3^4+3^5+...+3^{2023}\right)-\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(2D=\left(3^{2023}-1\right)\)
\(D=\left(3^{2023}-1\right):2\)
3D=3+3^2+...+3^2023
=>2D=3^2023-1
=>\(D=\dfrac{3^{2023}-1}{2}\)
1+1+200000-268-23x5=
ai biết giú mình cần gấp cho anh
 giú
giú
Giú
XI
1 more exciting
2 most boring
3 fathest
4 well
5 happier
6 worst
7 colder
8 most difficult
9 better
10 carefully
XII
1 C
2 C
3 B
4 A
5 A
6 B
9 A
10 C
9 B
Giú ạ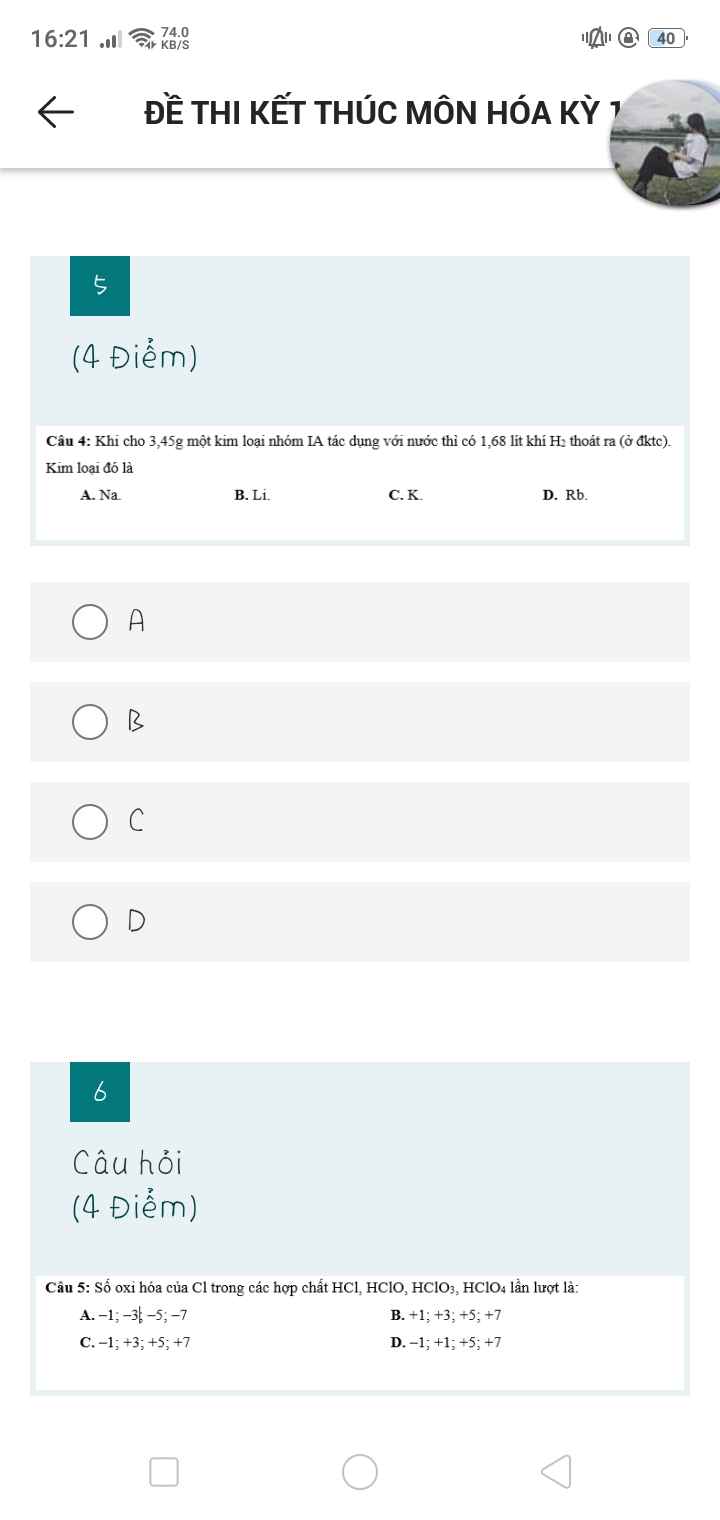
Câu 4 :
n H2 = 1,68/22,4 = 0,075(mol)
2R + 2HCl $\to$ 2RCl + H2
n R = 2n H2 = 0,15(mol)
=> M R = 3,45/0,15 = 23(Natri)
Câu 5 : D
Mn giú tui vs
Nhanh giú e ạ
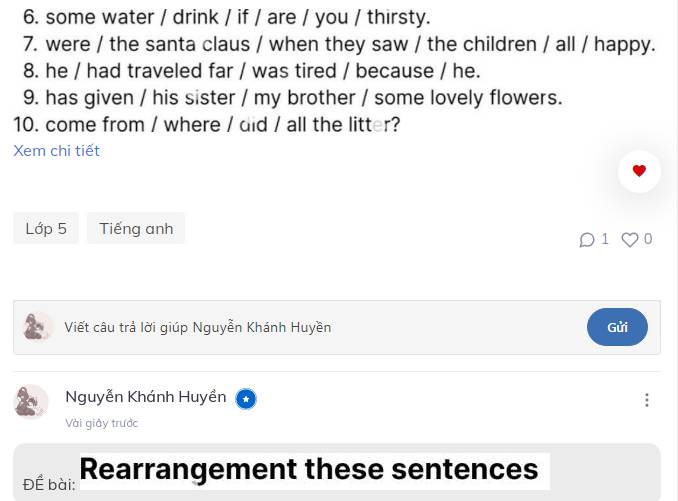
6 Drink some water if you are thirsty
7 The children were happy when they saw the Santa Clause
8 He was tired because he had traveled far
9 My brother has given his sister some lovely flowers
10 Where did all the litter come from?
 ecsresire 3 ạ giú mik
ecsresire 3 ạ giú mik
giú mk câu b với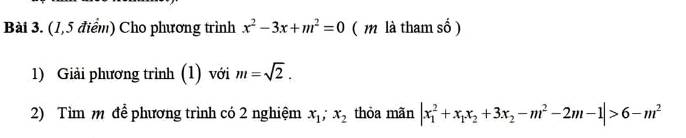
Lời giải:
Theo định lý Viet:
$x_1+x_2=3$
$x_1x_2=m^2$
Khi đó:
$|x_1^2+x_1x_2+3x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+x_1x_2+(x_1+x_2)x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+2x_1x_2+x_2^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |(x_1+x_2)^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |9-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |m^2+2m-8|> 6-m^2$
Nếu $m^2+2m-8\geq 0$ thì:
$m^2+2m-8> 6-m^2$
$\Leftrightarrow 2m^2+2m-14>0$
$\Leftrightarrow m^2+m-7>0$
$\Leftrightarrow m< \frac{-1-\sqrt{29}}{2}$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Kết hợp với $m^2+2m-8\geq 0$ suy ra $m\leq -4$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Nếu $m^2+2m-8<0$ thì:
$-(m^2+2m-8)> 6-m^2$
$\Leftrightarrow m< 1$
Kết hợp với $m^2+2m-8<0$ suy ra $-4< m< 1$
Vậy........