Cho \(\Delta ABC\) có 3 góc nhọn vẽ các đường cao BD CE.G ọi H,Ktheo thứ tự là hình chiếu của B và C trên đường ED .Chứng minh
a, EH=DK
b, \(S_{\Delta BEC}+S_{\Delta BDC}=S_{BHKC}\)
cho tam giác ABC có 3 góc nhọn , vẽ các đường cao BD,CE . Gọi H,K thứ tự hình chiếu của B và C trên đường thẳng ED
a. chứng minh : EH = DK
b. diện tích BEC + diện tích BDC + diện tích BHKC

Gọi M là trung điểm của BC, dễ dàng chứng minh được △MDE cân ở đỉnh M (MI là trung trực)
Gọi I là trung điểm của DE thì MI ⊥ DE
=>MI // BH //CE
MI là đường trung bình của hình thang BHKC, ta có IH = IK.
=> HI - IE = IK - ID
=> IE = ID
=> HE = DK
tam giác nhọn ABC, các đường cao BD, CE. Gọi H và K lần lượt là hình chiếu của B và C trên DE.
a/. Chứng minh: EM = DK
b/. Nếu ΔABC cân ở A thì tứ giác BCKH là hình gì?
a)

Chúc bạn học tốt!
1. Cho\(\Delta\)ABC, đường phân giác AM biết AB=5,AC=6,BC=7.Kẻ các đường cao MD,ME xuống AB,AC.Tính diện tích các \(\Delta\)ABM và \(\Delta\)ACM.
2. Cho \(\Delta\)ABC vuông tại A,đường cao AH. Có AC=5cm,AH=4cm.
a) Tính độ dài các yếu tố còn lại của \(\Delta\)ABC
b)Kẻ các đường cao HM,HN của \(\Delta\)ABH và \(\Delta\)ACH, tính \(\dfrac{S_{ABH}}{S_{ACH}}\)
c) Tính \(\dfrac{S_{ABC}}{S_{AMN}}\)
ΔABC vuông ở A, đường cao AH. Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC.
a/. Chứng minh rằng: AH=DE
b/. Gọi I và K theo thứ tự là trung điểm của HB và HC. Chứng minh rằng: DIKE là hình thang vuông
Tham khảo:
\(\Rightarrow\) Tứ giác \(DIEK\) là hình thang (định nghĩa hình thang) (đpcm).
Hình thang vuông là hình thang chỉ có 1 góc vuông thôi nhưng trong tứ giác \(DIEK\) có tận 2 góc vuông nên mình nghĩ chỉ suy ra là hình thang thôi.
Chúc bạn học tốt!
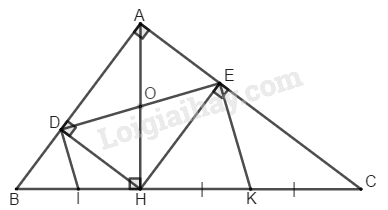
Cho tam giác ABC có góc A khác 90 độ và các góc B , C nhọn , đường cao AH. Vẽ các điểm D vá E sao cho AB là đường trung trực HD và AC là đường trung trực của HE.Gọi I và K theo thứ tự là giao điểm của DE với AB và AC . Tính góc AIC và góc AKB
gọi giao điểm của AB vs DH là N; giao điểm của AC vs EH là M
xét tam giác DIN và tam giác HIN = nhau(c.g.c) suy ra IN hay IB là phân giác góc DIH
xét tam giác MKH và tam giác MKE = nhau (c.g.c) suy ra kc là phân giác góc MKE
ta lại có HA là phân giác góc HIK( NA,MA là phân giác góc ngoài)
mà góc AHC=90 độ(gt) suy ra HC là phân giác góc ngoài tam giác HIK tại đỉnh H
mà KC là phân giác góc ngoài tam giác HIK tại đỉnh K
suy ra IC là phân giác góc KIH
mà IB là phân giác góc DIH
góc KIH + góc DIH=180 độ( kề bù) suy ra góc BIC=90 độ
suy ra góc AIC=90 độ
góc AKB cm tương tự = 90 độ
tuy mk ko biết chắc cách giải nhưng mk chắc bạn Đức làm sai rồi!
$\large\Delta{ADB} = \large\Delta{AEC} (c.g.c)$ (bạn tự chứng minh 2 tam giác này bằng nhau nhé!)
\Rightarrow $\widehat{BAD} = \widehat{EAC}$ (cặp góc tương ứng) (1)
Trên tia đối của tia DA lấy O sao cho DA = DO.
\Rightarrow $\large\Delta{ADE} = \large\Delta{ODB}$ (tự CMinh)
\Rightarrow $\hat{BOD} = \hat{DAE}$ (cặp góc tương ứng) ; AE = BO (cặp cạnh tương ứng)
Ta có :
$\hat{AEC} > \hat{ABE}$ (vì $\hat{AEC}$ là góc ngoài tại đỉnh E của tam giác AEB)
\Rightarrow $\hat{AEC} > \hat{ACE}$ (vì $\hat{ABC} = \hat{ACB}$ do tam giác ABC cân tại A)
\Rightarrow AC > AE (Quan hệ giữa cạnh và góc đối diện trong tam giác)
\Rightarrow AB > BO
\Rightarrow $\hat{BOD} > \hat{BAD}$ (quan hẹ giữa cạnh và góc đối diện trong tam giác)
\Rightarrow $\hat{DAE} > \hat{BAD}$ (2)
Từ (1) và (2) \Rightarrow đpcm
Cho tam giác ABC có 3 góc nhọn, các đường cao AD, BE, CF cắt nhau tại H.
a, Chứng minh: \(\Delta ABE\)đồng dạng với \(\Delta ACF\)
b, Chứng minh: HE.HB=HC.HF
c, Chứng minh: góc AEF= góc ABC
d, Chứng minh EB là tia phân giác của góc DEF
a, Xét △ABE vuông tại E và △ACF vuông tại F
Có: ∠BAC là góc chung
=> △ABE ᔕ △ACF (g.g)
b, Xét △HFB vuông tại F và △HEC vuông tại E
Có: ∠FHB = ∠EHC (2 góc đối đỉnh)
=> △HFB = △HEC (g.g)
\(\Rightarrow\frac{HF}{HE}=\frac{HB}{HC}\)
=> HF . HC = HE . HB
c, Vì △ABE ᔕ △ACF (cmt)
\(\Rightarrow\frac{AB}{AC}=\frac{AE}{AF}\)\(\Rightarrow\frac{AB}{AE}=\frac{AC}{AF}\)
Xét △ABC và △AEF
Có: \(\frac{AB}{AE}=\frac{AC}{AF}\)
∠BAC là góc chung
=> △ABC ᔕ △AEF (c.g.c)
=> ∠ABC = ∠AEF
d, Xét △BEC vuông tại E và △ADC vuông tại D
Có: ∠ACB là góc chung
=> △BEC ᔕ △ADC (g.g)
\(\Rightarrow\frac{BC}{AC}=\frac{EC}{DC}\)\(\Rightarrow\frac{BC}{EC}=\frac{AC}{DC}\)
Xét △ACB và △DCE
Có: \(\frac{BC}{EC}=\frac{AC}{DC}\)
∠ACB là góc chung
=> △ACB ᔕ △DCE (c.g.c)
=> ∠ABC = ∠DEC
Mà ∠ABC = ∠AEF (cmt)
=> ∠DEC = ∠AEF
Ta có: \(\hept{\begin{cases}\widehat{AEF}+\widehat{FEB}=\widehat{AEB}\\\widehat{CED}+\widehat{DEB}=\widehat{CEB}\end{cases}}\Rightarrow\hept{\begin{cases}\widehat{AEF}+\widehat{FEB}=90^o\\\widehat{CED}+\widehat{DEB}=90^o\end{cases}}\Rightarrow\widehat{FEB}=\widehat{DEB}\)
=> EB là phân giác \(\widehat{FED}\)
CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn
Cho ABC nhọn nội tiếp đường tròn (O,R).Các đường cao BD và CE cắt nhau tại H
a,Chứng minh:AEHD,BCED là các tứ giác nội tiếp đường tròn
b,Gọi M,N theo thứ tự là giao điểm thử 2 của đường tròn với BD và CE.Chứng minh MN song song ED
c,Chứng minh OA vuông góc ED
d,Kẻ tiếp tuyến Ax với đường tròn.CHứng minh xAN=EBD
e,gọi I là tâm đường tròn ngoại tiếp tam giác BCDE.Lấy điể F đối xứng với H qua điểm I.Chứng minh tứ giác ABFC nội tiếp
f,Chứng minh diện tích AHI=2. diện tích AOI
MỌI NGƯỜI LÀM GIÚP MÌNH CÂU CUỐI VỚI>MIK CẦN GẤP!!!!
d/ Gọi K, P lần lượt là hình chiếu của H,O lên AI
Xét tam giác AHF ta có :
O là trung điểm AF
I là trung điểm BC
=> OI là đường trung bình của tam giác AHF
=>\(\hept{\begin{cases}OI=\frac{1}{2}AH\\OI//AH\end{cases}}\)
Xét tam giác AHI ta có
\(\hept{\begin{cases}S_{AHI}=\frac{1}{2}HK.AI\\\sin H\widehat{A}I=\frac{HK}{AH}=>HK=AH.\sin H\widehat{AI}\end{cases}}\)(tam giác AHK vuông tại K )
=>\(S_{AHI}=\frac{1}{2}.AH.AI.sinH\widehat{A}I\)
Chứng minh tương tự cho tam giác AOI =>\(S_{AOI}=\frac{1}{2}.IO.IA.sinA\widehat{I}O\)
Ta có :
\(S_{AHI}=2.S_{AOI}\)
\(< =>\frac{1}{2}AH.AI.sinH\widehat{A}I=2.\frac{1}{2}IA.IO.sinA\widehat{IO}\)( Vì góc HAI = góc AIO do OI//AH nên sin của chúng = nhau)
\(< =>\frac{1}{2}AH=IO\left(LĐ\right)\)
Cái hệ thức này lớp 10 sẽ học nha bạn

bạn ơi phải chứng minh thêm A O F thẳng hàng với F thuộc đường tròn à
1) Cho ΔABC có góc B = góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng;
a) ΔADB=ΔADC
b) AB=AC
c) AD vuông góc với BC
2) Cho góc xOy; vẽ tia phân giác Ot của góc xOy. Trên tia Ot lấy điểm M bất kỳ; trên các tia Ox và Oy lần lượt lấy các điểm A và B sao cho OA=OB gọi H là giao điểm của AB và Ot. Chứng minh:
a) MA=MB
b) OM là đường trung trực của AB
1.a
Xét \(\Delta ADB;\Delta ADC\) có :
\(\widehat{B}=\widehat{C}\left(gt\right)\\ AB=AC\left(\widehat{B}=\widehat{C}\right)\\ \widehat{DAB}=\widehat{DAC}\left(gt\right)\\ \Rightarrow\Delta ADB=\Delta ADC\left(g-c-g\right)\)
b.
\(\Delta ADB=\Delta ADC\left(cmt\right)\\ \Rightarrow AB=AC\)
c.
\(\Delta ADB=\Delta ADC\left(cmt\right)\\ \Rightarrow\widehat{ADB}=\widehat{ADC}=90^0\\ \Rightarrow AD\perp BC\)
2.
Xét \(\Delta AOM;\Delta BOM\) có
\(OA=OB\left(gt\right)\\ \widehat{MOA}=\widehat{MOB}\left(gt\right)\\ OM\left(chung\right)\\ \Rightarrow\Delta MOA=\Delta MOB\left(c-g-c\right)\\ \Rightarrow MA=MB\)
b.
MA=MB
OA=OB
=> OM là đường trung trực AB
Bài 1 :
b) Do tam giác ABC có góc B = Góc C
=> Tam giác ABC cân tại A
<=> AB=AC
a) Xét tam giác ACB và tam giác ABD, ta có :
AD là cạnh chung
AB=AC ( Chứng minh trên )
\(\widehat{CA\text{D}}=\widehat{BA\text{D}}\) ( Do AD là tia phân giác góc A )
=> Tam giác ACB = Tam giác ABD. ( Góc-cạnh-góc )
c) Do tam giác ACB = Tam giác ABD ( Chứng minh trên )
=> \(\widehat{A\text{D}C}=\widehat{A\text{D}B}\) ( Hai góc tương ứng )
Mà hai góc này ở vị trí kề bù
=> AD vuông góc với BC
*Note : Câu trả lời của mình chưa chắc đã đúng.
Nhưng bạn nhớ đọc kĩ câu trả lời và áp dụng nhé. Có khi nó cũng giúp bạn hiểu ra vấn đề thì sao? Bạn đừng có chép khi không hiểu nha. Mục đích trả lời câu hỏi của mình là giúp những bạn gửi câu hỏi hiểu ra được bài và áp dụng nó vào trong những bài khác. Bạn cứ tìm hiểu kĩ bài đi nhé. Không hiểu chỗ nào cứ hỏi mình, mình tư vấn cho.Cho đường tròn (O) có đường kính AB =2R.Lấy điểm M,N thuộc (O) (A,M,N,B theo thứ tự đó). Gọi H là giao điểm của AN, BM ; K là hình chiếu của H lên BA.
a) Chứng minh AMHK nội tiếp
b) NK cắt (O) tại E. Chứng minh ME vuông góc AB
c) Các tiếp tuyến của (O) tại M và N cắt nhau tại I. Chứng minh I,H,K thẳng hàng
d) Lấy C đối xứng H qua I. Chứng minh C,M,A thẳng hàng và C,N,B thẳng hàng