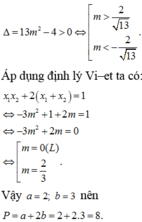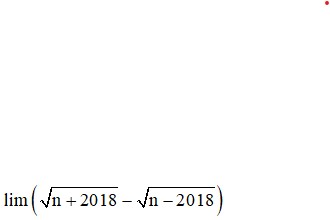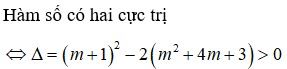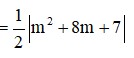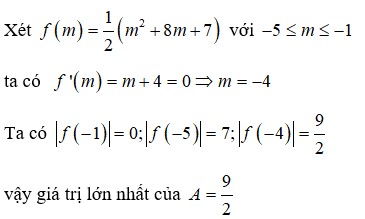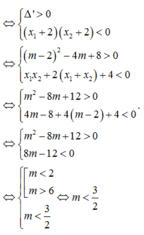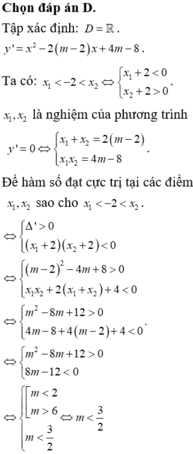cho y= -2x3 - 3(2a +1)x2 -6a(a+1)+2 có cực trị tại x1 ; x2 . khi đó trị tuyệt đối x1 - x2 là bao nhiêu

Những câu hỏi liên quan
Biết
a
b
(trong đó
a
b
là phân số tối giản,
a
,
b
∈
N
*
) là giá trị thực của tham số m để hàm số
y
2
x
3
-
3
m
x
2
-
6
(
3
m
2...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản, a , b ∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 m x 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P=a+2b.
![]()
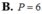
![]()
![]()
Biết
a
b
(trong đó
a
b
là phân số tối giản, a,b∈
N
*
) là giá trị thực của tham số m để hàm số
y
2
x
3
-
3
mx
2
-
6
(
3
m...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản, a,b∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 mx 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P= a+2b.
A. P=5.
B. P=6.
C. P=7.
D. P=8.
Cho hàm số
y
2
3
x
3
+
(
m
+
1
)
2
+
(
m
2
+
4
m
+
3
)
x
đạt cực trị tại
x
1
,
x...
Đọc tiếp
Cho hàm số y = 2 3 x 3 + ( m + 1 ) 2 + ( m 2 + 4 m + 3 ) x đạt cực trị tại x 1 , x 2 . Giá trị lớn nhất của biểu thức A = x 1 x 2 - 2 ( x 1 + x 2 ) bằng
A. 9 2
B. 9 2
C. 1
D. 4
Cho biết hàm số y =x^3 - (m-1).x^2 -x +2 có 2 điểm cực trị x1,x2 thoả mãn3(x1+x2)=2. Giá trị của m?
Lời giải:
$y'=3x^2-2(m-1)x-1$
Để hàm số có 2 điểm cực trị $x_1,x_2$ thì pt $y'=0$ có 2 nghiệm phân biệt $x_1,x_2$. Điều này xảy ra khi $\Delta'=(m-1)^2+3>0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=\frac{2(m-1)}{3}$
Khi đó:
$3(x_1+x_2)=2$
$\Leftrightarrow 2(m-1)=2$
$\Leftrightarrow m-1=1$
$\Leftrightarrow m=2$ (tm)
$\Leftright
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để hàm số:
y
1
3
m
x
3
-
(
m
-
1
)
x
2
+
3
(
m
-
2
)
x
+...
Đọc tiếp
Tìm các giá trị của tham số m để hàm số: y = 1 3 m x 3 - ( m - 1 ) x 2 + 3 ( m - 2 ) x + 1 6 đạt cực trị tại x 1 , x 2 thỏa mãn x 1 + 2 x 2 = 1
A. 1 - 6 2 < m < 1 + 6 2 .
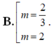
C. m ∈ 1 - 6 2 ; 1 + 6 2 \ 0 .
D. m = 2 .
Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

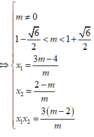

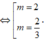
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của m để hàm số
y
x
3
3
-
(
m
-
2
)
x
2
+
(
4
m
-
8
)
x
+
m
+
1
đạt cực trị tại các điểm x1, x2 sao cho
x
1
-
2
x...
Đọc tiếp
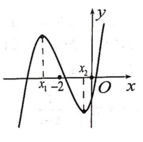
Tìm tất cả các giá trị thực của m để hàm số y = x 3 3 - ( m - 2 ) x 2 + ( 4 m - 8 ) x + m + 1 đạt cực trị tại các điểm x1, x2 sao cho x 1 < - 2 < x 2 .
A. m ⩾ 1 .
B. m > 1 2 .
C. m ⩽ 2 .
D. m < 3 2 .
Tìm tất cả các giá trị thực của m để hàm số
y
x
3
3
-
(
m
-
2
)
x
2
+
(
4
m
-
8
)
x
+
m
+
1
đạt cực trị tại các điểm x1, x2 sao cho
x
1
-
2
-...
Đọc tiếp
Tìm tất cả các giá trị thực của m để hàm số y = x 3 3 - ( m - 2 ) x 2 + ( 4 m - 8 ) x + m + 1 đạt cực trị tại các điểm x1, x2 sao cho x 1 < - 2 < - x 2
A. m ≥ 1
B. m > 1 2
C. m ≤ 2
D. m < 3 2
Tìm m để hàm số y = 1 phần 3 x mũ 3 - (m + 1) x^2 + ( m^2 + 2) x + m - 2 đạt cực trị tại x1 x2 thỏa x1 bình phương + X2 bình phương = 10
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
2
x
3
-
3
(
m
+
1
)
x
2
+
6
m
x
có hai điểm cực trị...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị A , B sao cho đường thẳng AB vuông góc với đường thẳng : y = x + 2 .
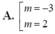

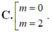
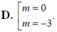
Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
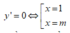
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
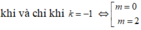
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y x+ 2. A. 0; 3 B. 2; 4 C. 0; 2 D. 1; 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
A. 0; 3
B. 2; 4
C. 0; 2
D. 1; 3
+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
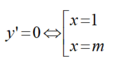
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 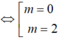
Chọn C.
Đúng 1
Bình luận (0)