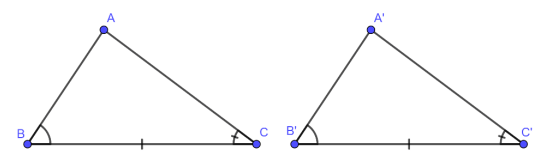
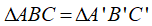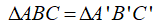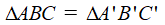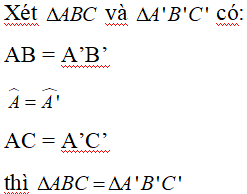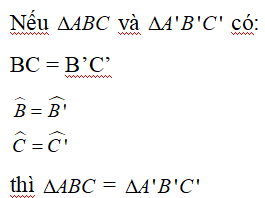Mọi người giúp mình nha nha ! cảm ơn mọi người nhiều !

Những câu hỏi liên quan
Mọi người giúp mình câu này nha...

 cảm ơn mọi người nhiều...
cảm ơn mọi người nhiều...
Do M là điểm chính giữa của cung AB \(\Rightarrow MA=MB\) (1)
Ta có \(\Lambda MAN=\Lambda MAB=\dfrac{1}{2}sđcungMB\) (\(\Lambda\) kí hiệu góc)
\(\Lambda MBC=\dfrac{1}{2}sđcungMB\) \(\Rightarrow\Lambda MAN=\Lambda MBC\)(2)
\(\Lambda AMN\) là góc chắn đường kính AB \(\Rightarrow\Lambda AMB=90^0\Rightarrow\Lambda AMN+\Lambda NMB=90^0\)
\(\Lambda NMC=90^0\Rightarrow\Lambda NMB+\Lambda BMC=90^0\) \(\Rightarrow\Lambda AMN=\Lambda BMC\)(3)
Từ (1) ,(2) và (3) \(\Rightarrow\Delta AMN=\Delta BMC\left(g.c.g\right)\)
Đúng 2
Bình luận (0)
Mọi người ơi !
Mọi người giúp mình nha !
Đặt tính rồi tính :
882 : 36 = ?
Cảm ơn mọi người nhiều lắm !
Xem thêm câu trả lời
 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người ơi giúp mình làm từ bài 44 đến 50 với nha mọi người mình cảm ơn nhiều
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
Đúng 3
Bình luận (1)
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi giúp mình với ạ, màu đỏ là đáp số đó nha mọi người, cảm ơn mọi người nhiều ạ 
Bài 3:
Điện trở tương đương: \(R=\dfrac{U}{I}=\dfrac{30}{0,5}=60\Omega\)
Điện trở R1: \(R_1=R-R_2=60-20=40\Omega\)
\(I=I_1=I_2=0,5A\left(R_1ntR_2\right)\)
Hiệu điện thế hai đầu mỗi điện trở:
\(U_1=R_1.I_1=40.0,5=20V\)
\(U_2=R_2.I_2=20.0,5=10V\)
Đúng 2
Bình luận (0)
Bài 2:
a. Ý nghĩa:
- Điện trở định mức của biến trở con chạy là 100Ω
- Cường độ dòng điện định mức của biến trở con chạy là 2A.
b. HĐT lớn nhất: \(U=R.I=100.2=200V\)
c. Chiều dài dây dẫn: \(R=p\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{p}=\dfrac{100.2.10^{-6}}{0,5.10^{-6}}=400m\)
Đúng 3
Bình luận (0)
Mọi người làm giúp mình bài 1,2 nha. Mình cảm ơn mn người rất nhiều
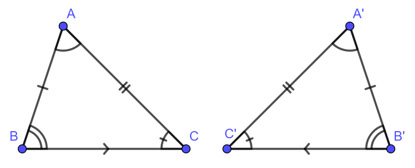
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác vuông
• Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
• Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
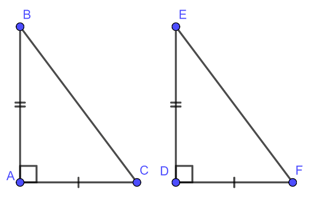
• Cạnh huyền – góc nhọn
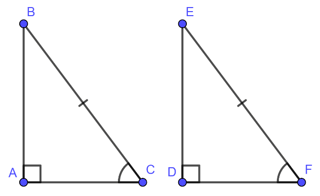
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
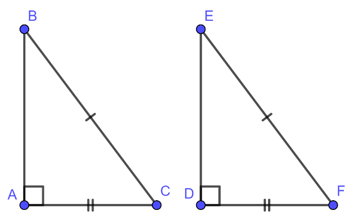
• Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác
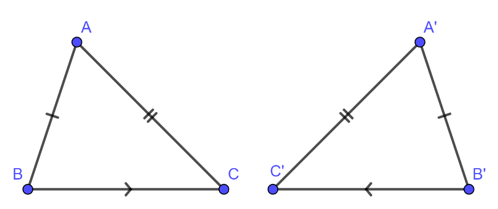
a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
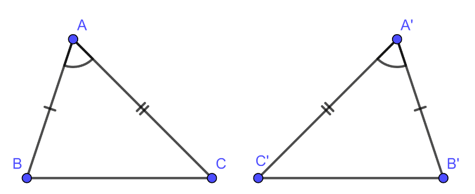
Xét 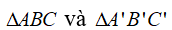
AB = A’B’
AC = A’C’
BC = B’C’
thì
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
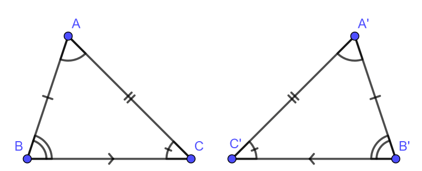
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
tik cho mình nha mình đc câu1 nè
Đúng 1
Bình luận (0)
hi mình là thành viên mới mong mọi người kết bạn và giúp đỡ mình nha cảm ơn mọi người nhiều
Xem thêm câu trả lời
Giúp mình nha mình đang cần gấp cảm ơn mọi người nhiều lắm. 
Bài 1:
a. $=2x(x-3)$
b. $=x^3(x+3)+(x+3)=(x^3+1)(x+3)=(x+1)(x^2-x+1)(x+3)$
c. $=64-(x^2-2xy+y^2)=8^2-(x-y)^2$
$=(8-x+y)(8+x-y)$
Đúng 1
Bình luận (0)
Bài 2:
$(x+5)(x+1)+(x-2)(x^2+2x+4)-x(x^2+x-2)$
$=x^2+6x+5+(x^3-2^3)-(x^3+x^2-2x)$
$=x^2+6x+5+x^3-8-x^3-x^2+2x$
$=8x-3$
Ta có đpcm.
Đúng 1
Bình luận (0)
Bài 4:
$P=a^3+a^2c-abc+b^2c+b^3$
$=a^2(a+c)-abc+b^2(b+c)$
$=a^2(-b)-abc+b^2(-a)=-a^2b-abc-b^2a$
$=-ab(a+c+b)=-ab.0=0$
Đúng 1
Bình luận (0)
(-4)^2 phần 16 = âm 64
mọi người giúp mình nha cảm ơn mọi người nhiều