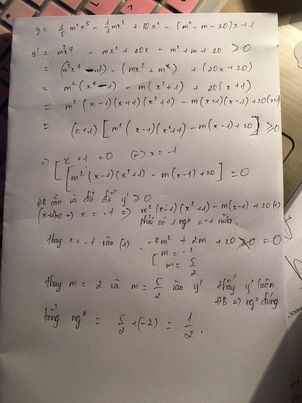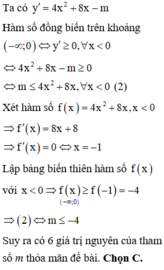Có bao nhiêu giá trị thực của tham số m để hàm số y = \(\left|x^2+mx+1\right|\) trên [-1;2] đạt giá trị nhỏ nhất bằng 1

Những câu hỏi liên quan
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số y=\(\sqrt{1-\left|2x^2+mx+m+15\right|}\). Có bao nhiêu giá trị của tham số m để hàm số xác định trên đoạn [1;3]
Bài 8. Cho hàm số \(y=\sqrt{1-\left|2x^2+mx+m+15\right|}\). Có bao nhiêu giá trị của tham số mđể hàm số xác định trên đoạn [1,3] .
Tổng tất cả các giá trị của tham số m để hàm số \(y=\dfrac{1}{5}m^2x^5-\dfrac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x+1\) đồng biến trên R bằng bao nhiêu?
Có bao nhiêu giá trị nguyên của tham số m \(\in\left(-20;20\right)\) để hàm số y = \(\dfrac{x-1}{x-m}\) nghịch biến trên khoảng \(\left(-\infty;2\right)\)
\(y'=\dfrac{x-m-x+1}{\left(x-m\right)^2}=\dfrac{1-m}{\left(x-m\right)^2}\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;2\right)\Leftrightarrow y'< 0\forall x\in\left(-\infty;2\right)\Leftrightarrow\left\{{}\begin{matrix}1-m< 0\\x\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge2\end{matrix}\right.\Rightarrow m\ge2\)
Có 19-2+1=18 giá trị nguyên của m thỏa mãn
Đúng 1
Bình luận (0)
Cho hàm số \(y=\dfrac{x^3}{3}-\left(m-1\right)x^2+3\left(m-1\right)x+1\). Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng \(\left(1;+\infty\right)\)
\(y'=x^2-2\left(m-1\right)x+3\left(m-1\right)\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta luôn có:
\(g\left(x\right)=x^2-2\left(m-1\right)x+3\left(m-1\right)\ge0\)
\(\Rightarrow\min\limits_{x>1}g\left(x\right)\ge0\)
Do \(a=1>0;-\dfrac{b}{2a}=m-1\)
TH1: \(m-1\ge1\Rightarrow m\ge2\)
\(\Rightarrow g\left(x\right)_{min}=f\left(m-1\right)=\left(m-1\right)^2-2\left(m-1\right)^2+3\left(m-1\right)\ge0\)
\(\Rightarrow\left(m-1\right)\left(4-m\right)\ge0\Rightarrow1\le m\le4\Rightarrow2\le m\le4\)
TH2: \(m-1< 1\Rightarrow m< 2\Rightarrow g\left(x\right)_{min}=g\left(1\right)=m\ge0\)
Vậy \(0\le m\le4\)
Đúng 0
Bình luận (0)
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
Cho hàm số
y
4
3
x
3
+
4
x
2
m
x
+
10
(1) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của tham số thực m lớn hơn -10 để hàm số (1) đồng biến trên khoảng
-
∞
;
0
A. 5 B. 4 C. 6 D. 7
Đọc tiếp
Cho hàm số y = 4 3 x 3 + 4 x 2 = m x + 10 (1) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của tham số thực m lớn hơn -10 để hàm số (1) đồng biến trên khoảng - ∞ ; 0
A. 5
B. 4
C. 6
D. 7
Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn - 2018 ; 2018 để hàm số y = x 3 - 6 x + m x + 1 đồng biến trên 1 ; + ∞
A. 2007
B. 2030
C. 2005
D. 2018