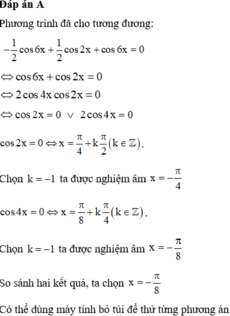giải phương trình : a) cosx×cos3x+sin2x×sin6x+sin4x×sin6x=0

Những câu hỏi liên quan
Giải phương trình:
\(\cos x.\cos3x-\sin2x.\sin6x-\sin4x.\sin6x=0\).
x=π/2+kπ
x=π/18+kπ/9
Xem thêm câu trả lời
giải phương trình : a) \(\cos x\times\cos3x+\sin2x\times\sin6x+\sin4x\times\sin6x=0\)
b) \(\cos x+\cos3x+2\cos5x=0\)
Nghiệm âm lớn nhất của phương trình:
sin
2
x
+
sin
4
x
.
sin
6
x
0
A
.
-
π
8
B
.
-
π
4
C
.
...
Đọc tiếp
Nghiệm âm lớn nhất của phương trình: sin 2 x + sin 4 x . sin 6 x = 0
A . - π 8
B . - π 4
C . - π 12
D . - π 6
1) giải pt:
a) cosx.cosx=cos2x.cos4x
b) cos5x.sin4x=cos3x.sin2x
c) sinx+sin2x=cosx+cos2x
d) sin2x+sin4x=sin6x
a/ Bạn coi lại vế trái đề bài, nhìn không hợp lý
b/ \(\Leftrightarrow\frac{1}{2}sin9x-\frac{1}{2}sinx=\frac{1}{2}sin5x-\frac{1}{2}sinx\)
\(\Leftrightarrow sin9x=sin5x\)
\(\Leftrightarrow\left[{}\begin{matrix}9x=5x+k2\pi\\9x=\pi-5x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{\pi}{14}+\frac{k\pi}{7}\end{matrix}\right.\)
c/ \(\Leftrightarrow sin2x-cos2x=cosx-sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow cos\left(\frac{3\pi}{4}-2x\right)=cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{3\pi}{4}-2x=x+\frac{\pi}{4}+k2\pi\\\frac{3\pi}{4}-2x=-x-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (1)
d/
\(\Leftrightarrow sin2x=sin6x-sin4x\)
\(\Leftrightarrow2sinx.cosx=2cos5x.sinx\)
\(\Leftrightarrow sinx\left(cosx-cos5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos5x=cosx\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\5x=x+k2\pi\\5x=-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{k\pi}{2}\\x=\frac{k\pi}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
9. Rút gọn các biểu thức sau
A= cos7x - cos8x - cos9x + cos10x / sin7x - sin8x - sin9x + sin10x
B = sin2x + 2sin3x + sin4x / sin3x +2sin4x + sin5x
C= 1+cosx + cos2x + cos3x / cosx + 2cos^2 . x -1
D = sin4x + sin5x + sin6x / cos4x + cos5x + cos6x
\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)
Đúng 0
Bình luận (0)
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
Giải phương trình :
\(2\sin6x-2\sin4x+\sqrt{3}\cos2x=\sqrt{3}+\sin2x\)
Từ phương trình ban đầu ta có : \(2\cos5x\sin x=\sqrt{3}\sin^2x+\sin x\cos x\)
\(\Leftrightarrow\begin{cases}\sin x=0\\2\cos5x=\sqrt{3}\sin x+\cos x\end{cases}\)
+) \(\sin x=0\Leftrightarrow x=k\pi\)
+)\(2\cos5x=\sqrt{3}\sin x+\cos x\Leftrightarrow\cos5x=\cos\left(x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\begin{cases}x=-\frac{\pi}{12}+\frac{k\pi}{2}\\x=\frac{\pi}{18}+\frac{k\pi}{3}\end{cases}\)
Đúng 0
Bình luận (0)
giải các pt
a) \(cosx+cos11x=cos6x\)
b) \(sin2x-cos5x=cosx-sin6x\)
c) \(sinx+sin2x+sin3x=cosx+cos2x+cos3x\)
a/
\(\Leftrightarrow2cos6x.cos5x=cos6x\)
\(\Leftrightarrow cos6x\left(2cos5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cos6x=0\\cos5x=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}6x=\frac{\pi}{2}+k2\pi\\5x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k\pi}{3}\\x=\pm\frac{\pi}{15}+\frac{k2\pi}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/
\(\Leftrightarrow sin2x+sin6x-\left(cos5x+cosx\right)=0\)
\(\Leftrightarrow2sin4x.cos2x-2cos3x.cos2x=0\)
\(\Leftrightarrow cos2x\left(sin4x-cos3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin4x=cos3x=sin\left(\frac{\pi}{2}-3x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\4x=\frac{\pi}{2}-3x+k2\pi\\4x=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{14}+\frac{k2\pi}{7}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow sinx+sin3x+sin2x=cosx+cos3x+cos2x\)
\(\Leftrightarrow2sin2x.cosx+sin2x=2cos2x.cosx+cos2x\)
\(\Leftrightarrow sin2x\left(2cosx+1\right)=cos2x\left(2cosx+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sin2x=cos2x=sin\left(\frac{\pi}{2}-2x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\frac{1}{2}\\2x=\frac{\pi}{2}-2x+k2\pi\\2x=2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\frac{2\pi}{3}+k2\pi\\x=\frac{\pi}{8}+\frac{k\pi}{2}\\\end{matrix}\right.\)
Đúng 0
Bình luận (0)