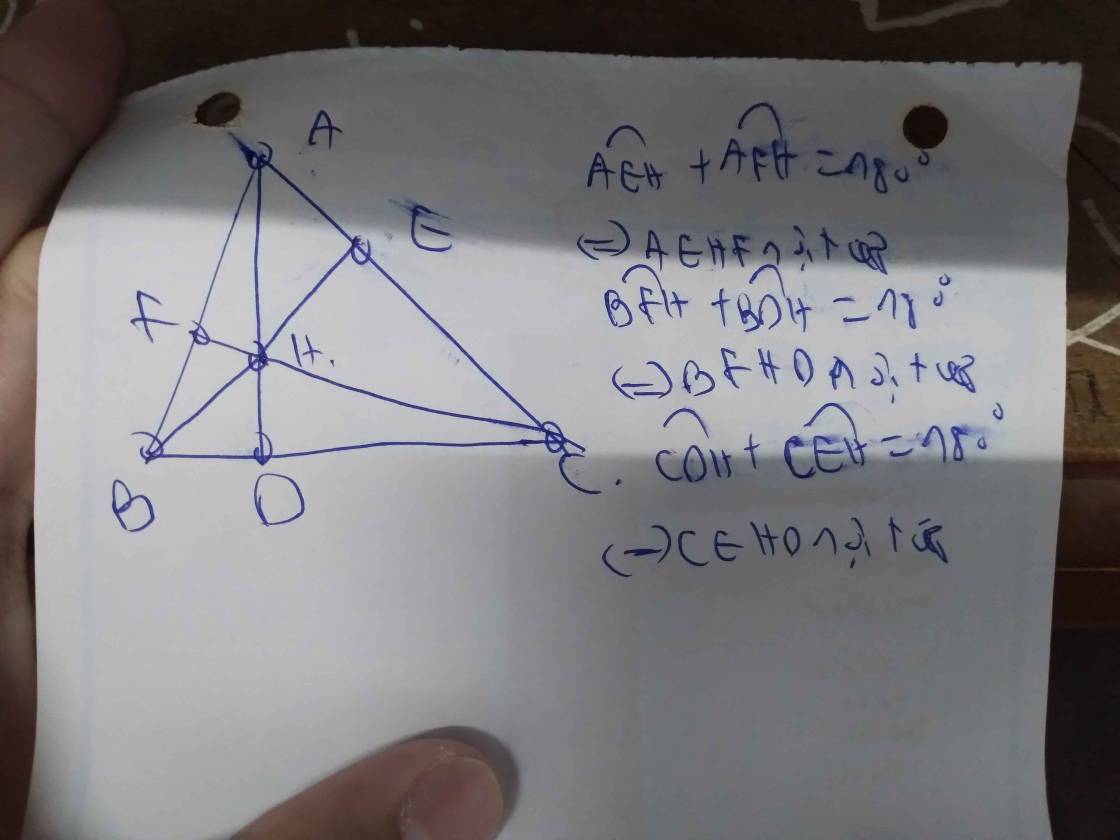
▲ABC, đường cao AD, BE, CF. Chỉ ra tất cả các tứ giác nội tiếp

Những câu hỏi liên quan
Cho tam giác ABC các đường cao AD,BE,CF cắt nhau tại H. Chỉ ra tất cả các tứ giác nội tiếp.
BFEC; AEDB; DCAF; AFHE; BFHD; CEHD
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H
a)Chứng minh tứ giác BFHD, BFEC nội tiếp
b) Chỉ ra các tứ giác còn lại nội tiếp được đường tròn
c) Chứng minh H là tâm của đường tròn nội tiếp tam giác EFD
d) Gọi M là trung điểm của BC. Chứng minh tứ giác EFDM nội tiếp
Xem chi tiết
a) Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) cùng nhìn cạnh BC một góc bằng 900
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 5
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.
A.AEHF
B. BFEC
C. AEDB
D. Cả A, B, C.
Đề: cho ∆ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF, cắt nhau tại H a) CM: tứ giác BCEF nội tiếp đường tròn và xác định tâm I của đường tròn ngoại tiếp tứ giác
Ta có \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BCEF nội tiếp đường tròn đường kính BC. Tâm I của đường tròn này là trung điểm của BC
Đúng 1
Bình luận (1)
Cho tam giác ABC nhọn (AB<AC) nội tiếp (o) đường kính Ak, các đường cao AD, BE, CF cắt nhau tại. Gọi M là trung điểm BC.
a) Cm: Tứ giác DMEF nội tiếp
Cho tam giác ABC nhọn nội tiếp (O) . Các đường cao AD, BE , và CF cắt nhau tại H . Đường thẳng EF cắt đường tròn ở I và K a) chứng minh : Tứ giác CDHE nội tiếp đường trònb) Chứng minh : AH . AD = AF . ABc) Kẻ tiếp tuyến Ax, chứng minh: BCEF nội tiếp. Từ đó chứng minh : Ax // IK
 h vẽ như sau:
h vẽ như sau:
Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H
A. tứ giác AEHF nội tiếp
b. tức giác BFEC nội tiếp
c. chúng minh OA vuông góc EF
a) Xét tứ giác AEHF có
\(\widehat{AFH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{AFH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
b) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
bài tập 1: cho tam giác abc có các đường cao ad, be, cf cắt nhau tại h. chứng minh rằng các tứ giác aehf, cdhf, behd nội tiếp.
Cho tam giac ABC có 3 góc nhọn ( AB<AC ) nội tiếp (O) . Các đường cao AD , BE , CF cắt nhau tại H . C/m : tứ giác BDEF nội tiếp