Các câu hỏi tương tự
Cho tam giác ABC (AB = AC) nội tiếp đường tròn tâm (O) các đường cao AG, BE, CF cắt nhau tại H. Chứng minh rằng tứ giác AEHF nội tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
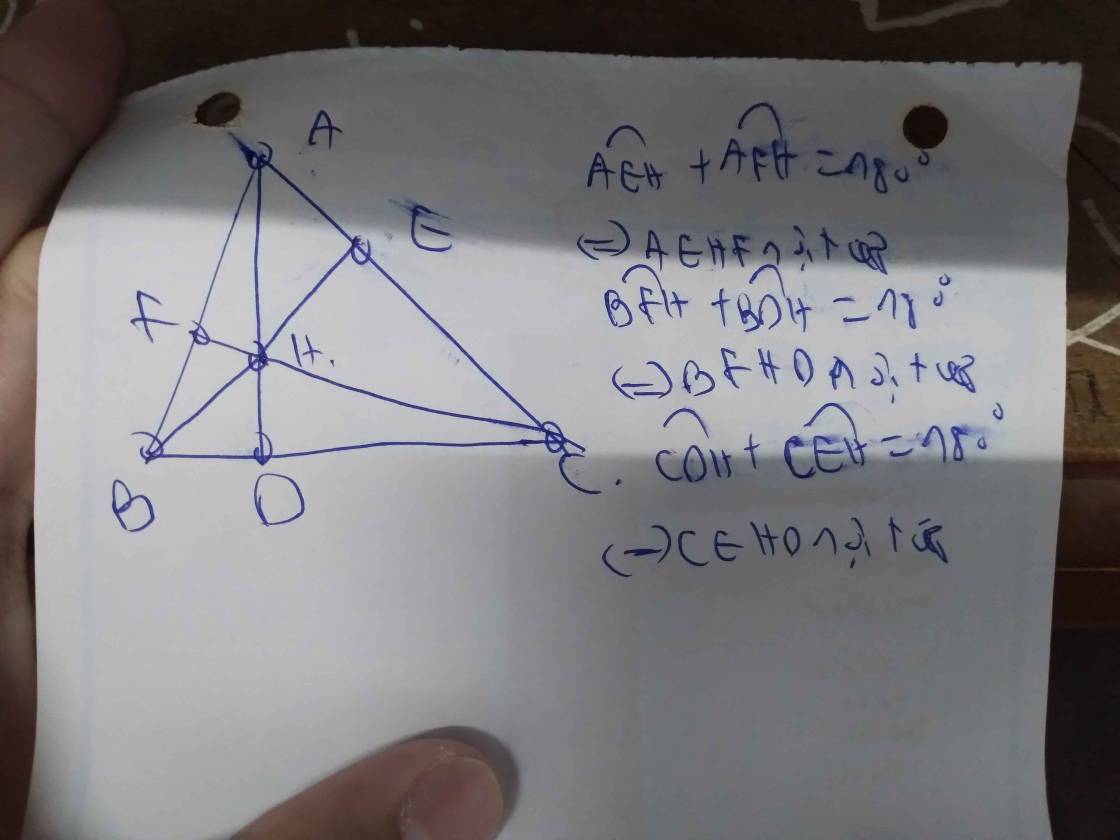
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
cho tam giác ABC có các góc đều nhọn và có ba đường cao AD, CF, BE cắt nhau tại H
a, chứng minh tứ giác BCEF, AEHF nội tiếp
b, Chứng minh EH.EB=EA.EC
c, chứng minh H là tâm dường tròn nội tiếp tam giác DEF
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H
A. tứ giác AEHF nội tiếp
b. tức giác BFEC nội tiếp
c. chúng minh OA vuông góc EF
cho tam giác ABC có ba góc nhọn nội tiếp (O) (ABCA) các đường cao AD, BE, CF cắt nhau tại H. a, Chứng minh các tứ giác AEHF, ACDF nội tiếp. b, Gọi I là điểm dối xứng của E qua BC, BC cắt AI, EI lần lượt tại L K. Vẽ LN vuuong góc với AC tại N. Chứng minh góc KNL góc DAL. c, Chứng minh ba điểm F,D,I thẳng hàng. d, NK cắt AI tại M. Chứng minh A là tâm đường tròn bàng tiếp trong góc M của tam giác DMN
Đọc tiếp
cho tam giác ABC có ba góc nhọn nội tiếp (O) (AB<CA) các đường cao AD, BE, CF cắt nhau tại H. a, Chứng minh các tứ giác AEHF, ACDF nội tiếp. b, Gọi I là điểm dối xứng của E qua BC, BC cắt AI, EI lần lượt tại L K. Vẽ LN vuuong góc với AC tại N. Chứng minh góc KNL= góc DAL. c, Chứng minh ba điểm F,D,I thẳng hàng. d, NK cắt AI tại M. Chứng minh A là tâm đường tròn bàng tiếp trong góc M của tam giác DMN
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H và lần lượt cắt đường tròn tại M, N, P. Chứng minh rằng:
1) Tứ giác BFEC và AEDB nội tiếp.
2) AE.AC = AF.AB.
3) Chứng minh H là tâm đường tròn nội tiếp tam giác EFD.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn(O).
Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. CMR:
a/. Các tứ giác AEHF, BCEF nội tiếp
b/ AD.BC = BE AC
c/. CMR BHM cân
Cho tam giác ABC có ba đường cao AD, BE, CF cắt nhau tại H. Biết ba góc
CAB
^
,
ABC
^
,
BCA
^
đều là góc nhọn. Gọi M là trung điểm của đoạn AH.1) Chứng minh tứ giác AEHF nội tiếp đường tròn. 2) Chứng minh CE.CA CD.CB.
Đọc tiếp
Cho tam giác ABC có ba đường cao AD, BE, CF cắt nhau tại H. Biết ba góc CAB ^ , ABC ^ , BCA ^ đều là góc nhọn. Gọi M là trung điểm của đoạn AH.
1) Chứng minh tứ giác AEHF nội tiếp đường tròn.
2) Chứng minh CE.CA = CD.CB.
cho tam giác ABC nhọn nội tiếp đường tròn O. Vẽ 2 đường cao BE và CF cắt nhau tại H.
a. Chúng minh tứ giác AEHF nội tiếp
b. chứng minh BCEF nội tiếp