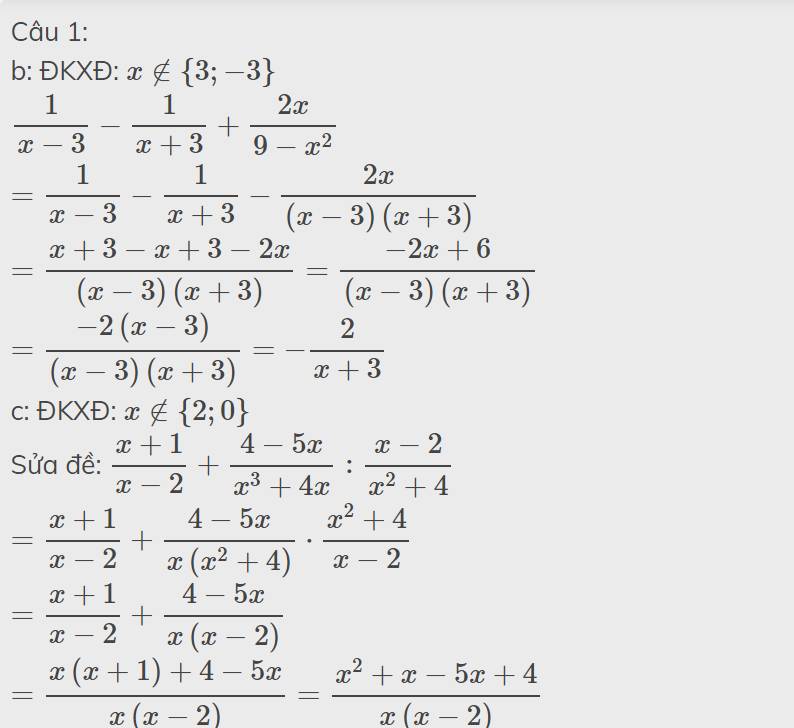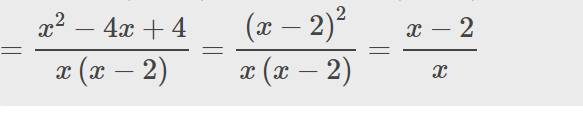b) x3 – x2 – 5x + 125

= (x3 + 125) - (x2 + 5x)

= (x + 5)(x2 - 5x + 25) - x(x + 5)

= (x + 5)(x2 - 5x + 25 - x)

= (x + 5)(x2 - 6x + 25)

Bài 1:

\(a,6x^2-15x^3y\\ b,=-\dfrac{2}{3}x^2y^3+\dfrac{2}{3}x^4y-\dfrac{8}{3}xy\)

Bài 2:

\(a,=20x^3-10x^2+5x-20x^3+10x^2+4x=9x\\ b,=3x^2-6x-5x+5x^2-8x^2+24=24-11x\\ c,=x^5+x^3-2x^3-2x=x^5-x^3-2x\)

câu d của bài 2 là của bài 1 nha mình để nhầm chỗ huhu

Lời giải:

a.

$=-2x^5+10x^4+2424x^3-x^3-3=-2x^5+10x^4+2423x^3-3$

b.

$=(x-5y)^2+2(x-5y)(x+y)+(x+y)^2$

$=[(x-5y)+(x+y)]^2=(2x-4y)^2=4x^2-16xy+16y^2$

a) P(x) = 7x² . (x² – 5x + 2 ) – 5x .(x³ – 7x² + 3x)

= 7x² . x² + 7x² . (-5x) + 7x² . 2 – [5x. x³ + 5x . (-7x²) + 5x . 3x]

= 7. (x² . x²) + [7.(-5)] . (x² . x) + (7.2).x²  – {5. (x.x³) + [5.(-7)]. (x.x²) + (5.3).(x.x)}

= 7x⁴ + (-35). x³ + 14x²  – [ 5x⁴ + (-35)x³ + 15x² ]

= 7x⁴ + (-35). x³ + 14x²   - 5x⁴ + 35x³ - 15x²

= (7x⁴ – 5x⁴) + [(-35). x³ + 35x³ ] + (14x² - 15x² )

= 2x⁴ + 0 - x² 

= 2x⁴ – x²

b) Thay x = \( - \dfrac{1}{2}\) vào P(x), ta được:

P(\( - \dfrac{1}{2}\)) = 2. (\( - \dfrac{1}{2}\))⁴ –  (\( - \dfrac{1}{2}\))² \))

 \(\begin{array}{l} = 2.\dfrac{1}{{16}} - \dfrac{1}{4} \\ = \dfrac{1}{8} - \dfrac{{2}}{8} \\ = \dfrac{-1}{8} \end{array}\)

2D

6

\(x^3+125=\left(x+5\right)\left(x^2-5x+25\right)\)

A là đa thức bậc 1

=>A=x+5

=>B=x^2-5x+25

=>Chọn A

Câu 2. M có bậc 2 + 7 = 9

Chọn D

Câu 6. x³ + 125 = x³ + 5³ = (x + 5)(x² - 5x + 25)

Chọn A

2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)

a) \(\left(x^5+4x^3-6x^2\right):4x^2\)

\(=\left(x^5:4x^2\right)+\left(4x^3:4x^2\right)+\left(-6x^2:4x^2\right)\)

\(=\dfrac{1}{4}x^3+x-\dfrac{3}{2}\)

b) 

Vậy \(\left(x^3+x^2-12\right):\left(x-2\right)=x^2+3x+6\)

c) (-2x⁵ : 2x²) + (3x² : 2x²) + (-4x^3 : 2x^2)

= \(-x^3+\dfrac{3}{2}-2x\)

d) \(\left(x^3-64\right):\left(x^2+4x+16\right)\)

\(=\left(x-4\right)\left(x^2+4x+16\right):\left(x^2+4x+16\right)\)

\(=x-4\)

(dùng hẳng đẳng thức thứ 7)

Bài 2 :

a) 3x(x - 2) - 5x(1 - x) - 8(x² - 3)

= 3x² - 6x - 5x + 5x² - 8x² + 24

= (3x² + 5x² - 8x²) + (-6x - 5x) + 24 

= -11x + 24

b) (x - y)(x² + xy + y²) + 2y³

= x³ - y³ + 2y³

= x³ + y³ 

c) (x - y)² + (x + y)² - 2(x - y)(x + y)

= (x - y)² - 2(x - y)(x + y) + (x + y)²

= [(x - y) + x + y)² = [x - y + x + y] = (2x)² = 4x²

Bài 1 :

a]=  \(\frac{1}{4}\)x³ + x - \(\frac{3}{2}\).

b] => [x³ + x² -12 ] = [ x² +3 ][x-2] + [-6]

c]= -x³ -2x +\(\frac{3}{2}\).

d] = [ x³ - 64 ]  = [ x² + 4x + 16][ x- 4].