a: \(70a+84b-20ab-24b^2\)

\(=\left(70a+84b\right)-\left(20ab+24b^2\right)\)

\(=14\left(5a+6b\right)-4b\left(5a+6b\right)\)

\(=\left(5a+6b\right)\left(14-4b\right)\)

\(=2\left(7-2b\right)\left(5a+6b\right)\)

b: \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)

\(=\left(x^2y+x^2z\right)+\left(xy^2+xz^2\right)+\left(y^2z+yz^2\right)+3xyz\)

\(=x^2\left(y+z\right)+x\left(y^2+z^2\right)+yz\left(y+z\right)+3xyz\)

\(=x^2\left(y+z\right)+x\left(y^2+z^2\right)+yz\left(y+z\right)+2xyz+xyz\)

\(=x^2\left(y+z\right)+x\left(y^2+z^2+2yz\right)+yz\left(y+z+x\right)\)

\(=x^2\left(y+z\right)+x\left(y+z\right)^2+yz\left(y+z+x\right)\)

\(=\left(y+z\right)\cdot x\left(x+y+z\right)+yz\left(y+z+x\right)\)

\(=\left(y+z+x\right)\cdot\left(xy+xz+yz\right)\)

c: \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+2xyz\)

\(=\left(x^2y+x^2z\right)+\left(xy^2+xz^2+2xyz\right)+\left(y^2z+yz^2\right)\)

\(=x^2\left(y+z\right)+x\left(y^2+z^2+2xz\right)+yz\left(y+z\right)\)

\(=\left(y+z\right)\left(x^2+yz\right)+x\left(y+z\right)^2\)

\(=\left(y+z\right)\left(x^2+yz+xy+xz\right)\)

\(=\left(y+z\right)\left(x+z\right)\left(x+y\right)\)

b) x2y + 4xy + 4y – y3

= y(x2 + 4x + 4 - y2)

= y[(x2 + 4x + 4) - y2]

= y[(x + 2)2 - y2]

= y(x + 2 + y)(x + 2 - y)

a) \(70a+84b-20ab-24b^2\)

\(=\left(70a+84b\right)-\left(20ab+24b^2\right)\)

\(=14\left(5a+6b\right)-4b\left(5a+6b\right)\)

\(=\left(5a+6b\right)\left(14-4b\right)\)

\(=2\left(5a+6b\right)\left(7-2b\right)\)

b) \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)

\(=\left(x^2y+xy^2+xyz\right)+\left(x^2z+xyz+xz^2\right)+\left(xyz+y^2z+yz^2\right)\)

\(=xy\left(x+y+z\right)+xz\left(x+y+z\right)+yz\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)

c) \(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+2xyz\)

\(=\left(x^2y+xy^2\right)+\left(xz^2+yz^2\right)+\left(x^2z+2xyz+y^2z\right)\)

\(=xy\left(x+y\right)+z^2\left(x+y\right)+z\left(x^2+2xy+y^2\right)\)

\(=xy\left(x+y\right)+z^2\left(x+y\right)+z\left(x+y\right)^2\)

\(=\left(x+y\right)\left[xy+z^2+z\left(x+y\right)\right]\)

\(=\left(x+y\right)\left(xy+z^2+xz+yz\right)\)

\(=\left(x+y\right)\left[\left(xy+yz\right)+\left(xz+z^2\right)\right]\)

\(=\left(x+y\right)\left[y\left(x+z\right)+z\left(x+z\right)\right]\)

\(=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

a, 70a + 84b - 20ab - 24b²

 = 14.(5a + 6b) - 4b(5a + 6b)

= (5a + 6b).(14 - 4b) 

a, 70a + 84b - 20ab - 24b²

 = (70a + 84b) - (20ab + 24b²)

= 14.(5a + 6b) - 4b.(5a + 6b)

= (5a + 6b).(14 - 4b)

\(=xy\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(xy-7\right)\)

\(a,=2xy\left(\dfrac{1}{3}x-y+2\right)\\ b,=\left(2x-3y\right)\left(2x+3y\right)-\left(2x+3y\right)=\left(2x+3y\right)\left(2x-3y-1\right)\)

b: Ta có: \(4x^2-9y^2-2x-3y\)

\(=\left(2x-3y\right)\left(2x+3y\right)-\left(2x+3y\right)\)

\(=\left(2x+3y\right)\left(2x-3y-1\right)\)

\(a,=\left(x-y\right)\left(x+y\right)+11\left(x-y\right)=\left(x-y\right)\left(x+y+11\right)\\ b,=\left(x+z\right)\left(x^2-xz+z^2\right)+y\left(x^2+z^2-xz\right)\\ =\left(x^2-xz+z^2\right)\left(x+y+z\right)\)

a. x² - y² + 11x - 11y

= (x + y)(x - y) + 11(x - y)

= (x + y + 11)(x - y)

b. Mik ko hiểu đề lắm

a: \(6x^2-3x\)

\(=3x\cdot2x-3x\)

=3x(2x-1)

b: \(15x^5y^4+10x^3y^3-5xy\)

\(=5xy\cdot3x^4y^3+5xy\cdot2x^2y^2-5xy\cdot1\)

\(=5xy\left(3x^4y^3+2x^2y^2-1\right)\)

c: \(x^2y+4xy+4y\)

\(=y\cdot x^2+y\cdot4x+y\cdot4\)

\(=y\left(x^2+4x+4\right)=y\left(x+2\right)^2\)

\(x^3-x^2y+7x-7y=\left(x^3-x^2y\right)+\left(7x-7y\right)=x^2\left(x-y\right)+7\left(x-y\right)=\left(x-y\right)\left(x^2+7\right)\)

\(x^3-x^2y+7x-7y\)

\(=x^2\left(x-y\right)+7\left(x-y\right)\)

\(=\left(x-y\right)\cdot\left(x^2+7\right)\)

`@` `\text {Ans}`

`\downarrow`

`a,`

`3x^2 + 6xy + 3y^2 - 3z`

`= 3*x^2 + 3*2xy + 3y^2 - 3z`

`= 3(x^2 + 2xy + y^2 - z)`

`b,`

`x^3 + x^2y - x^2z - xyz`

`= x(x + y)(x-z)`

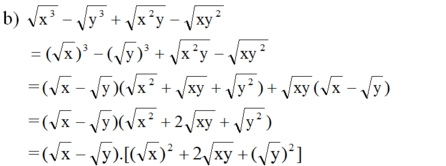
= (√x - √y)(√x + √y)2

= (√x - √y)(√x + √y)(√x + √y)

= (x - y)(√x + √y)