Cho hình dưới
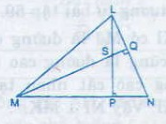
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
a/ Chứng minh NS vuông góc LM.
b/ Khi góc LMP = 50o, hãy tính góc MSP và góc PSQ.
NS lak gì?
LM lak gì?
Thiếu đề rồi bạn ơi
Cho hình 57.
Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.
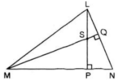
Hình 57
+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:

Cho hình 57 :
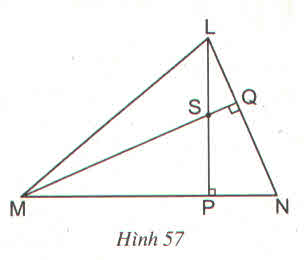
a) Chứng minh \(NS\perp LM\)
b) Khi \(\widehat{LNP}=50^0\), hãy tính góc MSP và góc PSQ
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay SN ⊥ ML
cho tam giac MNk duong cao MQ,KP cat nhau tai S
CM:a,NS vuông góc MK
b,Nếu KNP=50.Tính goc MSP va goc PSQ
Xét tam giác MNK có
MQ vuông góc với MK
KB vuông góc với MN
MQ cắt KB tại S
=> S là trực tâm của tam giác MNK
=> NS vuông góc với MK
Ta có ^PNS + ^ PSN = ^SNQ+^NSQ = 90 độ
=> ^PNS + ^ PSN +^SNQ+^NSQ=180\(^0\)
MÀ ^PNS+^SNQ = 50 độ
=> ^PSN+^NSQ = 130 độ hay ^PSQ = 130 độ
Cho tam giác ABC . Hai đường cao BM và CN cắt nhau tại H.
a. Chứng minh rằng AH vuông góc BC.
b. Khi góc BAC = 70 độ . Hãy tính góc BHNvà góc MHN.
c. Khi góc ACB = 50 độ . Hãy tính góc AHM.
a: XétΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH vuông góc với BC
b: \(\widehat{MHN}=360^0-90^0-90^0-70^0=110^0\)
=>\(\widehat{BHN}=70^0\)
Cho hình vẽ. Biết Ax // Cz, góc BAx = 500, góc CBy = 400, góc zCt = 400.
a) Góc BAx và góc ABy ở vị trí nào ? Góc CBy và góc zCt ở vị trí nào ?
b) Chứng minh By // Cz
c) Kẻ tia phân giác Cm của góc zCB cắt By tại K. Tính số đo góc BKC
chiếu 1 tia sáng SI hợp với phương nằm ngang gương một góc 30 như hình vẽ . tia phản xạ Ỉ có phương thẳng đứng từ trrne xuống dưới
a, vẽ tia phản xạ xác định vị trí đặt gương
b, tính góc phản xạ , góc tới , góc hợp bởi tia phản xạ và tia tới 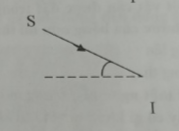
b,
\(i=90^o-30=60^o\)
\(i=i'\Leftrightarrow i'=60^o\)
\(i+i'=60^o+60^o=120^o\)
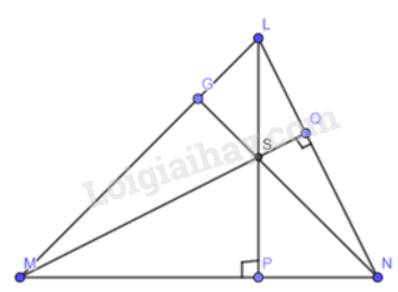
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Tham khảo:
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\( \Rightarrow \)Đường cao từ đỉnh N cũng đi qua S
\( \Rightarrow \)NS là đường cao của tam giác MNL
\( \Rightarrow \) NS vuông góc với ML tại G (là chân đường cao)
Cho góc xAy = 500. Gọi Ax' là tia đối của tia Ax; Ay' là tia đối của tia Ay.
a) Vẽ hình theo yêu cầu.
b) Tính góc x'Ay' và góc x'Ay.
c) Gọi Am là tia phân giác của góc xAy; Am' là tia phân giác của x'Ay'. Chứng minh Am và Am' là hai tia đối nhau.
CÁC BẠN GIẢI CHI TIẾT BÀI NÀY GIÚP MÌNH NHÉ! CẢM ƠN CÁC BẠN RẤT NHIỀU! 🤧🙏💖