Đề thiếu hay gì rồi bạn, trong đề đâu có điểm c

\(i=90^o-40^o=50^o\)

\(i=i'\Leftrightarrow i'=50^o\)

\(\Rightarrow D\)

D. 50^o

D

Hình vẽ đâu bạn?

a: Xét ΔDEK và ΔDFK có

DE=DF

EK=FK

DK chung

Do đó: ΔDEK=ΔDFK

b: Ta có: ΔDEF cân tại D

mà DK là đường trung tuyến

nên DK là đường phân giác

c: \(\widehat{F}=\widehat{E}=50^0\)

\(\widehat{EDF}=180^0-2\cdot50^0=80^0\)

\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)

                   \(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)

                   \(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)

\(Xét\) \(\Delta ABCvà\Delta DEFcó\)

\(\widehat{A}=\widehat{D}\left(=50^0\right)\)

AB=DE

AC=DF

\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)

Vậy \(\Delta ABC=\Delta DEF\)

Ko có góc C kìa bn

A và B là 1 đoạn thẳng, ko có giao nhau

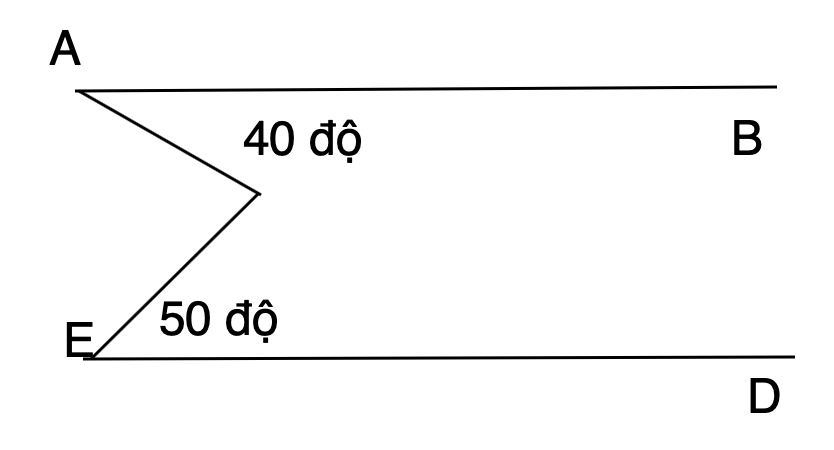
Kẻ 1 đường thẳng t qua C song song với AB và ED.

=> \(\widehat{tCA}=\widehat{A}=40^o\) (so le trong)

\(\widehat{tCE}=\widehat{E}=50^o\) (so le trong)

Ta có: \(\widehat{C}=40^o+50^o=90^o\)

=> \(AC\perp CE\)

a) Vì điểm D nằm giữa hai điểm A và C nên ta có:

AC=AD+CD

hay AC=4+3=7(cm)

Vậy: AC=7cm

b) Trên cùng một nửa mặt phẳng bờ chứa tia BA, ta có: \(\widehat{ABD}< \widehat{ABC}\left(30^0< 50^0\right)\)

nên tia BD nằm giữa hai tia BA,BC

\(\Leftrightarrow\widehat{ABD}+\widehat{CBD}=\widehat{ABC}\)

\(\Leftrightarrow\widehat{DBC}=\widehat{ABC}-\widehat{ABD}=50^0-30^0\)

hay \(\widehat{DBC}=20^0\)

Vậy: \(\widehat{DBC}=20^0\)