Giúp mik câu 2 vs ạ. Camon ạ

Những câu hỏi liên quan
Giúp mik mấy câu này vs ạ=((. Mik camon nhìuuu


Giúp mik mấy câu này vs ạ=((. Mik camon nhìuuu

Giúp mik vs, nếu ai thấy đc bài này thì hãy giúp mik vs ạ. Mik camon mn
Ai đặt 10 câu ghép cho mik vs ạ?
E camon nhiều
Đứa bé ngày càng hư,gia đình họ rất buồn phiền về nó.
Hễ con chó mà đi chậm, con khỉ lại cấu hai tai con chó giật giật.
Thời tiết càng khô hanh,da dẻ càng dễ bị khô nẻ
Thu qua,đông đến
Vì nhà nghèo quá,chú phải bỏ học
Trời càng về đêm,không gian càng tĩnh mịch
Tôi đã nói nhưng anh ấy không chịu nghe
Hãy viết 1 đoạn văn khoảng 10 - 12 câu, ghi lại cảm nghĩ của em về bài thơ "Buổi sáng nhà em" của Trần Đăng Khoa
Ae oiiii !!!Nhx ng có đầu óc lm Văn ơi, viết giùm mik đoạn này vs ikkk ạ ! Mik đang cần gấy giúp mik vs ạ !! Camon nhìu
**Tham khảo**
Bài thơ " Buổi sáng nhà em" của Trần Đăng Khoa là một bài thơ viết về cảnh buổi sáng sớm tinh mơ nên nhân vật " em" nhìn thấy rất nhiều cảnh đẹp và hoạt động của người trong gia đình. Hình ảnh bà vấn tóc, bố xách điếu, mẹ tát nước không chỉ người trong gia đình mà còn những sự vật mà nhân vật kể đến con mèo rửa mặt, con gaf cục tác, quả na mở mắt, đàn chuối vẫy tay, hàng tre chải tóc. Đang là những hoạt động quen thuộc và gần gũi với em. Yêu thay những sự gần gũi giản dị này. Thấy cuộc sống vô cùng bình yên nhưng cũng đầy màu sắc.
Đúng 2
Bình luận (0)
Mn giúp mik câu i,k,m ạ. Mik camon nhìuu
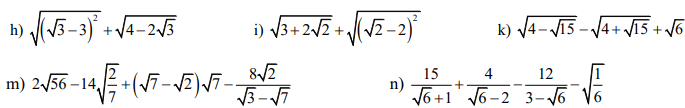
i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)
k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)
m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)
\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)
\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)
Đúng 1
Bình luận (0)
Lời giải:
i.
\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)
k.
\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)
\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)
\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)
m.
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)
\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)
Đúng 0
Bình luận (0)

Mn giúp mik câu 3 với 8 ạ, camon nhiu:3333
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Thay \(x=4-2\sqrt{3}\) vào P, ta được:
\(P=\dfrac{2\left(\sqrt{3}-1\right)+1}{\sqrt{3}-1+1}=\dfrac{2\sqrt{3}-2+1}{\sqrt{3}}=\dfrac{2\sqrt{3}-1}{\sqrt{3}}=\dfrac{6-\sqrt{3}}{3}\)
Đúng 1
Bình luận (2)
 giúp tớ vs tớ đg cần gấp ạ lm đc câu nào hay câu đấy ạ ( lm hết đc càng tốt có lời giải nha ) camon trccc ạ
giúp tớ vs tớ đg cần gấp ạ lm đc câu nào hay câu đấy ạ ( lm hết đc càng tốt có lời giải nha ) camon trccc ạ
Bài 1: - \(\dfrac{5}{7}\) x \(\dfrac{31}{33}\) + \(\dfrac{-5}{7}\) x \(\dfrac{2}{33}\) + 2\(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) \(\times\) ( \(\dfrac{31}{33}\) + \(\dfrac{2}{33}\)) + 2 + \(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) + 2 + \(\dfrac{5}{7}\)
= 2
Đúng 1
Bình luận (0)
2, \(\dfrac{3}{14}\): \(\dfrac{1}{28}\) - \(\dfrac{13}{21}\): \(\dfrac{1}{28}\) + \(\dfrac{29}{42}\): \(\dfrac{1}{28}\) - 8
= (\(\dfrac{3}{14}\) - \(\dfrac{13}{21}\) + \(\dfrac{29}{42}\)) : \(\dfrac{1}{28}\) - 8
= \(\dfrac{2}{7}\) x 28 - 8
= 8 - 8
= 0
Đúng 1
Bình luận (0)
3, \(\dfrac{37}{43}\) . \(\dfrac{17}{29}\) - \(\dfrac{21}{41}\).\(\dfrac{1}{2}\) + \(\dfrac{9}{58}\): 1\(\dfrac{6}{37}\) - \(\dfrac{6}{29}\): 1\(\dfrac{20}{21}\)
= \(\dfrac{37}{43}\). \(\dfrac{17}{29}\) - \(\dfrac{21}{41}\) . \(\dfrac{1}{2}\) + \(\dfrac{9}{58}\).\(\dfrac{37}{43}\) - \(\dfrac{6}{29}\).\(\dfrac{21}{41}\)
= (\(\dfrac{37}{43}\).\(\dfrac{17}{29}\) + \(\dfrac{9}{58}\).\(\dfrac{37}{43}\)) - (\(\dfrac{21}{41}\).\(\dfrac{1}{2}\) + \(\dfrac{6}{29}\).\(\dfrac{21}{41}\))
= \(\dfrac{37}{43}\).( \(\dfrac{17}{29}\) + \(\dfrac{9}{58}\)) - \(\dfrac{21}{41}\).( \(\dfrac{1}{2}\) + \(\dfrac{6}{29}\))
= \(\dfrac{37}{43}\).\(\dfrac{43}{58}\) - \(\dfrac{21}{41}\).\(\dfrac{41}{58}\)
= \(\dfrac{37}{58}\) - \(\dfrac{21}{58}\)
= \(\dfrac{16}{58}\)
= \(\dfrac{8}{29}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
câu 13:viết chương trình nhập 2 số nguyên khác nhau từ bàn phím và innhai số nguyên đó theo thứ tự tăng dần.
giúp mik vs ạ ![]()
mik xin camon
#include <bits/stdc++.h>
using namespace std;
long long a,b;
int main()
{
cin>>a>>b;
cout<<min(a,b)<<" "<<max(a,b);
return 0;
}
Đúng 0
Bình luận (0)
Var a,b:integer;
Begin
Write('Nhap a = ');readln(a);
Write('Nhap b = ');readln(b);
If a >= b then write(b,' ; ', a)
Else write(a,' ; ',b);
Readln;
End.
Đúng 1
Bình luận (0)




















