\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Câu 1

a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)

b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)

Bài 2

a) \(7x^2+14xy=7x\left(x+2y\right)\)

b) \(3x+12-\left(x^2+4x\right)=-x^2-x+12=\left(-x+3\right)\left(x+4\right)\)

c) \(x^2-2xy+y^2=\left(x-y\right)^2\)

d) \(x^2-2x-15=x^2+3x-5x-15=\left(x+3\right)\left(x-5\right)\)

1.

a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)

\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)

\(\Leftrightarrow x^3+3x^2+2x-6=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)

b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)

\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)

Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)

\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)

1c/

\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)

\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)

\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn

Vậy pt có nghiệm duy nhất \(x=-1\)

2.

a. \(x^4-x^3+x^2+x^2-x+1=0\)

\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)

\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)

Vậy pt vô nghiệm

b.

\(x^4+x^3+x^2+x+1=0\)

\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)

\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)

Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)

Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có

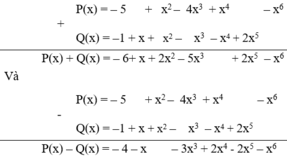
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6

P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6

a) x⁴ + 2x² + 1

= (x²)² + 2.x².1 + 1²

= (x² + 1)²

b) 4x² - 12xy + 9y²

= (2x)² - 2.2x.3y + (3y)²

= (2x - 3y)²

c) -x² - 2xy - y²

= -(x² + 2xy + y²)

= -(x + y)²

d) (x + y)² - 2(x + y) + 1

= (x + y)² - 2.(x + y).1 + 1²

= (x - y + 1)²

e) x³ - 3x² + 3x - 1

= x³ - 3.x².1 + 3.x.1² - 1³

= (x - 1)³

g) x³ + 6x² + 12x + 8

= x³ + 3.x².2 + 3.x.2² + 2³

= (x + 2)³

h) x³ + 1 - x² - x

= (x³ + 1) - (x² + x)

= (x + 1)(x² - x + 1) - x(x + 1)

= (x + 1)(x² - x + 1 - x)

= (x + 1)(x² - 2x + 1)

= (x + 1)(x - 1)²

k) (x + y)³ - x³ - y³

= (x + y)³ - (x³ + y³)

= (x + y)³ - (x + y)(x² - xy + y²)

= (x + y)[(x + y)² - x² + xy - y²]

= (x + y)(x² + 2xy + y² - x² + xy - y²)

= (x + y).3xy

= 3xy(x + y)

a, Sửa đề:

\(3x^2-\sqrt3 x+\dfrac14(dkxd:x\geq0)\\=(x\sqrt3)^2-2\cdot x\sqrt3\cdot\dfrac12+\Bigg(\dfrac12\Bigg)^2\\=\Bigg(x\sqrt3-\dfrac12\Bigg)^2\)

b, 

\(x^2-x-y^2+y\\=(x^2-y^2)-(x-y)\\=(x-y)(x+y)-(x-y)\\=(x-y)(x+y-1)\)

c,

\(x^4+x^3+2x^2+x+1\\=(x^4+x^3+x^2)+(x^2+x+1)\\=x^2(x^2+x+1)+(x^2+x+1)\\=(x^2+x+1)(x^2+1)\)

d,

\(x^3+2x^2+x-16xy^2\\=x(x^2+2x+1-16y^2)\\=x[(x+1)^2-(4y)^2]\\=x(x+1-4y)(x+1+4y)\\Toru\)

Bài 1

a/ \(x\left(x^2+1\right)+2\left(x^2+1\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^2+1\right)=0\Rightarrow x=-2\)

b/

\(\Leftrightarrow x^3-6x^2+9x+5x^2-30x+45=0\)

\(\Leftrightarrow x\left(x-3\right)^2+5\left(x-3\right)^2=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-3\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)

1.

c/ \(\Leftrightarrow x^3+2x^2+2x+x^2+2x+2=0\)

\(\Leftrightarrow x\left(x^2+2x+2\right)+x^2+2x+2=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+2=0\left(vn\right)\end{matrix}\right.\)

d/

\(\Leftrightarrow x^4+x^3-2x^2-x^3-x^2+2x+4x^2+4x-8=0\)

\(\Leftrightarrow x^2\left(x^2+x-2\right)-x\left(x^2+x-2\right)+4\left(x^2+x-2\right)=0\)

\(\Leftrightarrow\left(x^2-x+4\right)\left(x^2+x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+4=0\left(vn\right)\\x^2+x-2=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Bài 1:

e/ \(\Leftrightarrow x^4+2x^2-8x+5=0\)

\(\Leftrightarrow x^4-2x^3+x^2+2x^3-4x^2+2x+5x^2-10x+5=0\)

\(\Leftrightarrow x^2\left(x-1\right)^2+2x\left(x-1\right)^2+5\left(x-1\right)^2=0\)

\(\Leftrightarrow\left(x^2+2x+5\right)\left(x-1\right)^2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+5=0\left(vn\right)\\x=1\end{matrix}\right.\)

Bài 2:

a/ Đặt \(x^2-5x=t\)

\(t^2+10t+24=0\Rightarrow\left[{}\begin{matrix}t=-4\\t=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-5x=-4\\x^2-5x=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-5x+4=0\\x^2-5x+6=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=4\\x=2\\x=3\end{matrix}\right.\)

 P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3

= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5

= – x6 + x4 – 4x3 + x2 – 5.

= – 5+ x2 – 4x3 + x4 – x6

Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1

= 2x5 – x4 + (x3 – 2x3) + x2 + x –1

= 2x5 – x4 – x3 + x2 + x –1.

= –1+ x + x2 – x3 – x4 + 2x5

a) \(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\)

\(=\dfrac{1}{x+2}+\dfrac{5}{2x^2+4x-x-2}\)

\(=\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{2x\left(x+2\right)-\left(x+2\right)}\)

\(=\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2}{2x-1}\)

\(---\)

b) \(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\) (sửa đề)

\(=\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2x+2}{x^2-x+1}\)

\(---\)

c) \(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{1-x}{\left(1-x\right)\left(1+x\right)}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{1+x+1-x}{1^2-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2\left(1+x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{2\left(1-x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2+2x^2+2-2x^2}{1-x^4}+\dfrac{4}{1+x^4}\)

\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}\)

\(=\dfrac{4\left(1+x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}+\dfrac{4\left(1-x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}\)

\(=\dfrac{4+4x^4+4-4x^4}{1-x^8}\)

\(=\dfrac{8}{1-x^8}\)

#\(Toru\)

\(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\\ =\dfrac{1}{x+2}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2}{2x-1}\)

__

`x^3+1` chứ cậu nhỉ?

\(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x-1\right)\left(x^2-x+1\right)}\\ =\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x-1\right)}{x^2-x+1}\)

__

Alo đề nghị viết đề một cách chính xác