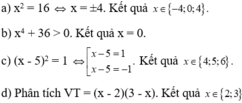(x2+4)2 - 16x2

Những câu hỏi liên quan
Câu 1: x2 + 2 xy + y2 bằng:A. x2 + y2 B.(x + y)2 C. y2 – x2 D. x2 – y2Câu 2: (4x + 2)(4x – 2) bằng:A. 4x2 + 4 B. 4x2 – 4 C. 16x2 + 4 D. 16x2 – 4Câu 3: 25a2 + 9b2 - 30ab bằng:A.(5a-9b)2 B.(5a – 3b)2 C.(5a+3b)2 D.(5a)2 – (3b)2Câu 4: 8x3 +1 bằngA.(2x+1).(4x2-2x+1) B. (2x-1).(4x2+2x+1) C.(2x+1)3 D.(2x)3-13Câu 5:Thực hiện phép n...
Đọc tiếp
Câu 1: x2 + 2 xy + y2 bằng:
A. x2 + y2 B.(x + y)2 C. y2 – x2 D. x2 – y2
Câu 2: (4x + 2)(4x – 2) bằng:
A. 4x2 + 4 B. 4x2 – 4 C. 16x2 + 4 D. 16x2 – 4
Câu 3: 25a2 + 9b2 - 30ab bằng:
A.(5a-9b)2 B.(5a – 3b)2 C.(5a+3b)2 D.(5a)2 – (3b)2
Câu 4: 8x3 +1 bằng
A.(2x+1).(4x2-2x+1) B. (2x-1).(4x2+2x+1) C.(2x+1)3 D.(2x)3-13
Câu 5:Thực hiện phép nhân x(3x2 + 2x - 5) ta được:
A.3x3 - 2x2 – 5x B. 3x3 + 2x2 – 5x C. 3x3 - 2x2 +5x D. 3x3 + 2x2 + 5x
câu 1 B
câu 2 D
câu 3 ko bt
câu 4 x=-1/2; x = -(căn bậc hai(3)*i-1)/4;x = (căn bậc hai(3)*i+1)/4;
câu 5 x=-5/3, x=0, x=1
Đúng 1
Bình luận (0)
Câu 1: x2 + 2 xy + y2 bằng:
A. x2 + y2 B.(x + y)2 C. y2 – x2 D. x2 – y2
Câu 2: (4x + 2)(4x – 2) bằng:
A. 4x2 + 4 B. 4x2 – 4 C. 16x2 + 4 D. 16x2 – 4
Câu 3: 25a2 + 9b2 - 30ab bằng:
A.(5a-9b)2 B.(5a – 3b)2 C.(5a+3b)2 D.(5a)2 – (3b)2
Câu 4: 8x3 +1 bằng
A.(2x+1).(4x2-2x+1) B. (2x-1).(4x2+2x+1) C.(2x+1)3 D.(2x)3-13
Câu 5:Thực hiện phép nhân x(3x2 + 2x - 5) ta được:
A.3x3 - 2x2 – 5x B. 3x3 + 2x2 – 5x C. 3x3 - 2x2 +5x D. 3x3 + 2x2 + 5x
Đúng 1
Bình luận (0)
(x-y)2-4
9-(x-y)2
(x2+4)2-16x2
\(\left(x-y\right)^2-4=\left(x-y-2\right)\left(x-y+2\right)\)
\(9-\left(x-y\right)^2=\left(3-x+y\right)\left(3+x-y\right)\)
\(\left(x^2+4\right)^2-16x^2=\left(x^2-4x+4\right)\left(x^2+4x+4\right)=\left(x-2\right)^2\left(x+2\right)^2\)
Đúng 1
Bình luận (0)
\((X-y)^2-4=(x-y-2)(x-y+2)\)\((X^2+4)^2-16x^2=(x^2+4)^2-(4x)^2=(x^2+4-4x)(x^2+4+4x)\)
\(9-(x-y)^2=(3-x+y)(3+x-y)\)
Đúng 0
Bình luận (2)
a)(x-y)2-4=(x-y)2-22=(x-y-2)(x-y+2)
b)9-(x-y)2=32-(x-y)2=(3-x+y)(3+x-y)
c)(x2+4)2-16x2=(x2+4)2-(4x)2=(x2+4-4x)(x2+4+4x)=(x-2)2(x+2)2=(x2-2)2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
4-x=2(x-4)2
(x2+1)(x-2)+2x=4
x4-16x2=0
`4-x=2(x-4)^2`
`<=>4-x=2(x^2-8x+16)`
`<=> 4-x=2x^2 - 16x+32`
`<=> 4-x-2x^2+16x-32=0`
`<=> -2x^2 +15x-28=0`
`<=> -(2x^2-15x+28)=0`
`<=>-(2x^2-7x-8x+28)=0`
`<=> - [x(2x-7) - 4(2x-7)]=0`
`<=> -(2x-7)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}-2x+7=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}-2x=-7\\x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\)
__
`(x^2 +1) (x-2)+2x=4`
`<=> x^3 -2x^2 +x-2+2x-4=0`
`<=> x^3 -2x^2 +3x-6=0`
`<=> (x^3+3x)-(2x^2+6)=0`
`<=> x(x^2 +3) -2(x^2+3)=0`
`<=>(x^2+3)(x-2)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=2\end{matrix}\right.\)
__
`x^4 -16x^2=0`
`<=> x^2 (x^2 -16)=0`
`<=>x^2(x-4)(x+4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Đúng 4
Bình luận (0)
\(4-x=2\left(x-4\right)^2\)
\(\Leftrightarrow4-x=2\left(x^2-8x+16\right)\)
\(\Leftrightarrow4-x=2x^2-16x+32\)
\(\Leftrightarrow2x^2-15x+28=0\)
\(\Leftrightarrow2x^2-7x-8x+28=0\)
\(\Leftrightarrow x\left(2x-7\right)-4\left(2x-7\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-7\\x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\)
___________
\(\left(x^2+1\right)\left(x-2\right)+2x=4\)
\(\Leftrightarrow x^3-2x^2+x-2+2x=4\)
\(\Leftrightarrow x^3-2x^2+3x-2-4=0\)
\(\Leftrightarrow x^3-2x^2+3x-6=0\)
\(\Leftrightarrow x^2\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-3\left(\text{vô lý}\right)\\x=2\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow x=2\)
________________
\(x^4-16x^2=0\)
\(\Leftrightarrow\left(x^2\right)^2-\left(4x\right)^2=0\)
\(\Leftrightarrow\left(x^2-4x\right)\left(x^2+4x\right)=0\)
\(\Leftrightarrow x\left(x-4\right)x\left(x+4\right)=0\)
\(\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x-4=0\\x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
6x3-9x2
25x2-0,09
X2-x-y2-y
(x2+4)2-16x2
\(6x^3-9x^2=3x^2\left(2x-3\right)\\ 25x^2-0,09=\left(5x-0,3\right)\left(5x+0,3\right)\\ x^2-x-y^2-y=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\\ \left(x^2+4\right)^2-16x^2=\left(x^2-4x+4\right)\left(x^2+4x+4\right)=\left(x-2\right)^2\left(x+2\right)^2\)
Đúng 1
Bình luận (0)
Bài 7: Phân tích đa thức thành nhân tử:
a, 4x2 - 1
b, x2 -3y2
c, 9x2 -1/4
d, (x-y)2 -4
e, 9 - (x-y)2
f, (x2 + 4)2 - 16x2
a) \(4x^2-1\)
\(=\left(2x\right)^2-1^2\)
\(=\left(2x-1\right)\left(2x+1\right)\)
b) \(x^2-3y^2\)
\(=x^2-\left(y\sqrt{3}\right)^2\)
\(=\left(x-y\sqrt{3}\right)\left(x+y\sqrt{3}\right)\)
c) \(9x^2-\dfrac{1}{4}\)
\(=\left(3x\right)^2-\left(\dfrac{1}{2}\right)^2\)
\(=\left(3x-\dfrac{1}{2}\right)\left(3x+\dfrac{1}{2}\right)\)
d) \(\left(x-y\right)^2-4\)
\(=\left(x-y\right)^2-2^2\)
\(=\left(x-y-2\right)\left(x-y+2\right)\)
e) \(9-\left(x-y\right)^2\)
\(=3^2-\left(x-y\right)^2\)
\(=\left(3+x-y\right)\left(3-x+y\right)\)
f) \(\left(x^2+4\right)^2-16x^2\)
\(=\left(x^2+4\right)^2-\left(4x\right)^2\)
\(=\left(x^2-4x+4\right)\left(x^2+4x+4\right)\)
\(=\left(x-2\right)^2\left(x+2\right)^2\)
Đúng 3
Bình luận (0)
a)4x2-4y2-20x+20y
b)16x2-25+(4x-5)
c)(x+5y)3
e)x2+4x+4-y2
g)x2-3x-4
\(a,4x^2-4y^2-20x+20y=4\left(x^2-y^2\right)-\left(20x-20y\right)=4\left(x-y\right)\left(x+y\right)-20\left(x-y\right)=\left(x-y\right)\left(4x+4y-20\right)=4\left(x-y\right)\left(x+y-5\right)\\ b,16x^2-25+\left(4x-5\right)=\left(4x-5\right)\left(4x+5\right)+\left(4x-5\right)=\left(4x-5\right)\left(4x+5+1\right)=\left(4x-5\right)\left(4x+6\right)=2\left(4x-5\right)\left(2x+3\right)\)
\(c,\left(x+5y\right)^3=x^3+15x^2y+75xy^2+125y^3\\ e,x^2-4x+4-y^2=\left(x-2\right)^2-y^2=\left(x-y-2\right)\left(x+y-2\right)\\ g,x^2-3x-4=\left(x^2-4x\right)+\left(x-4\right)=x\left(x-4\right)+\left(x-4\right)=\left(x+1\right)\left(x-4\right)\)
Đúng 1
Bình luận (0)
.Tìm x biết:
a) 3x(x – 2) – x + 2 = 0
b) x3 – 6x2 + 12x – 8 = 0
c) 16x2 – 9(x + 1)2
d) x2 (x – 1) – 4x2 + 8x – 4 = 0
\(a,\Leftrightarrow\left(x-2\right)\left(3x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-2\right)^3=0\Leftrightarrow x-2=0\Leftrightarrow x=2\\ c,\Leftrightarrow\left(4x-3x-3\right)\left(4x+3x+3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(7x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{7}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 5
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử.
a) 4x2 – 1 b) 25x2 - 0,09
d) (x - y)2 - 4
e) 9 - (x - y)2
f) (x2 + 4)2 - 16x2
\(a,4x^2-1\)
\(=\left(2x\right)^2-1^2\)
\(=\left(2x-1\right)\left(2x+1\right)\)
\(b,25x^2-0,09\)
\(=\left(5x\right)^2-\left(0,3\right)^2\)
\(=\left(5x-0,3\right)\left(5x+0,3\right)\)
\(d,\left(x-y\right)^2-4\)
\(=\left(x-y\right)^2-2^2\)
\(=\left(x-y-2\right)\left(x-y+2\right)\)
\(e,9-\left(x-y\right)^2\)
\(=3^2-\left(x-y\right)^2\)
\(=\left[3-\left(x-y\right)\right]\left[3+\left(x-y\right)\right]\)
\(=\left(3-x+y\right)\left(3+x-y\right)\)
\(=\left(-x+y+3\right)\left(x-y+3\right)\)
\(f,\left(x^2+4\right)^2-16x^2\)
\(=\left(x^2+4\right)^2-\left(4x\right)^2\)
\(=\left(x^2+4-4x\right)\left(x^2+4+4x\right)\)
\(=\left(x^2-2\cdot x\cdot2+2^2\right)\left(x^2+2\cdot x\cdot2+2^2\right)\)
\(=\left(x-2\right)^2\left(x+2\right)^2\)
#\(Toru\)
Đúng 2
Bình luận (1)
`#3107`
a)
`4x^2 - 1`
`= (2x)^2 - 1^2`
`= (2x - 1)(2x + 1)`
b)
`25x^2 - 0,09`
`= (5x)^2 - (0,3)^2`
`= (5x - 0,3)(5x + 0,3)`
d)
`(x - y)^2 - 4`
`= (x - y)^2 - 2^2`
`= (x - y - 2)(x - y + 2)`
e)
`9 - (x - y)^2`
`= 3^2 - (x - y)^2`
`= (3 - x + y)(3 + x - y)`
f)
`(x^2 + 4)^2 - 16x^2`
`= (x^2 + 4)^2 - (4x)^2`
`= (x^2 - 4x + 4)(x^2 + 4x + 4)`
`= (x - 2)^2 * (x + 2)^2`
_____
Tất cả các câu trên bạn sử dụng hđt:
`A^2 - B^2 = (A - B)(A + B)`
\(#MaiChangLaAnhDau..\)
Đúng 2
Bình luận (3)
Tìm x, biết: a)
x
4
-
16
x
2
0; c)
x
8
+
36
x
4
0; b)
(
x
-
5
)
3
- x + 5...
Đọc tiếp
Tìm x, biết:
a) x 4 - 16 x 2 =0; c) x 8 + 36 x 4 =0;
b) ( x - 5 ) 3 - x + 5 = 0; d) 5(x - 2 ) - x 2 + 4 = 0.