Hình 3.8 có A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ . Chứng tỏ rằng a // b.

Hình 3.8 có A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ . Chứng tỏ rằng a // b.

Ta có A 1 ^ + A 2 ^ = B 1 ^ + B 2 ^ = 180 ° ⇒ 2 A 1 ^ + 2 A 2 ^ = 2 B 1 ^ + 2 B 2 ^ (1)
Mặt khác: A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ (2)
Cộng từng vế các đẳng thức (1) và (2) được 3 A 1 ^ = 3 B 1 ^ ⇒ A 1 ^ = B 1 ^
=> a // b vì có cặp góc so le trong bằng nhau
1. Cho a > 0 , b > 0 và a > b , chứng tỏ rằng : 1/a < 1/b
2. Cho a,b là hai số bất kì , chứng tỏ rằng : ( a + b )2/2 ≥ 2ab
3. Cho a,b là hai số bất kì , chứng tỏ rằng : a2 + b2/2 ≥ ab
2.
\(\dfrac{\left(a+b\right)^2}{2}\ge2ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) ( đúng )
Tương tự.......................
1. Xét hiệu : \(\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{b-a}{ab}\)
Lại có: b - a < 0 ( a > b)
ab >0 ( a>0, b > 0)
\(\Rightarrow\dfrac{b-a}{ab}< 0\)
Vậy: \(\dfrac{1}{a}< \dfrac{1}{b}\)
2. Xét hiệu : \(\dfrac{\left(a+b\right)^2}{2}-2ab=\dfrac{a^2+2ab+b^2-4ab}{2}=\dfrac{\left(a-b\right)^2}{2}\ge0\)
Vậy : \(\dfrac{\left(a+b\right)^2}{2}\ge2ab\) Xảy ra đẳng thức khi a = b
3. Xét hiệu : \(\dfrac{a^2+b^2}{2}-ab=\dfrac{a^2+b^2-2ab}{2}=\dfrac{\left(a-b\right)^2}{2}\ge0\)
Vậy : \(\dfrac{a^2+b^2}{2}\ge ab\) Xảy ra đẳng thức khi a = b
Cho hình vẽ, biết : A ^ = 60 0 ; B ^ 1 = 1 2 B ^ 2 . Chứng tỏ rằng a//b
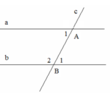
Ta có: B ^ 1 + B ^ 2 = 180 0 . ( Kề bù), mà B ^ 1 = 1 2 B ^ 2 nªn B ^ 1 = 180 0 : 3 = 60 0
⇒ A ^ 1 = B ^ 1 = 60 0
Do đó a//b ( vì có cặp góc so le trong bằng nhau).
a) chứng tỏ rằng 2^2016+3.8^671 chia hết cho 11
b) hãy so sánh (-9)^4.2^15 và 16^2.6^8
các bạn giúp mình với nha
a) Cho P = 1 + 3 + 32 + 33 +.......+ 3101. Chứng tỏ rằng P⋮13.
b) Cho B = 1 + 22 + 24 +.......+ 22020. Chứng tỏ rằng B ⋮ 21.
c) Cho A = 2 + 22 + 23 +........+ 220. Chứng tỏ A chia hết cho 5.
d) Cho A = 1 + 4 + 42 + 43 +..........+ 498. Chứng tỏ A chia hết cho 21.
e) Cho A = 119 + 118 + 117 +.........+ 11 + 1. Chứng tỏ A chia hết cho 5.
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
a. chứng tỏ rằng 3 điểm O; A(1;-2); B(2;-4) thẳng hàng
b.Chứng tỏ rằng 4 điểm O; A(1; 3); B(-2:-6); C(-1;-3) thẳng hàng
Lời giải:
Gọi PT đường thẳng $AB$ là: \(y=ax+b\)
Ta có: \(\left\{\begin{matrix} -2=a.1+b\\ -4=a.2+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=-2\\ b=0\end{matrix}\right.\)
\(\Rightarrow y=-2x\)
Xét điểm O(0;0) thấy \(0=-2.0\Rightarrow O\in (AB)\)
Do đó O,A,B thẳng hàng
b) Gọi phương trình đường thẳng AB là: \(y=ax+b\)
\(\Rightarrow \left\{\begin{matrix} 3=a.1+b\\ -6=a(-2)+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=3\\ b=0\end{matrix}\right.\)
\(\Rightarrow y=3x\)
Xét điểm O(0;0) có \(0=3.0\Rightarrow O\in (AB)\)
Xét điểm C(-1;-3) có \(-3=3.(-1)\Rightarrow C\in (AB)\)
Do đó O, A, B, C thẳng hàng.
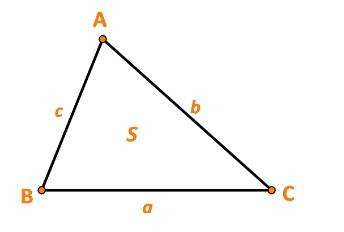
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
a) Từ định lí cosin, chứng tỏ rằng:
\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)
b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)
\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)
Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)
b) Ta có: \(S = \frac{1}{2}bc\sin A\)
Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)
\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)
Cho ab = 1. Chứng tỏ rằng: a^5 + b^5 = (a^3+b^3)(a^2+b^2) - ( a+b)
Xét VP: (a3+b3)(a2+b2) - (a+b)
= a5 + b5 + a3b2 + a2b3 - (a+b)
= a5 + b5 + a2b2(a+b) - (a+b)
= a5 + b5 + (a+b) - (a+b)
= a5 + b5 = VP (đpcm)