Tại sao f'(t)>0 suy ra được mcosx-sinx=2(1-sinx) vậy ạ

Cho hàm số y = (m + 1)sinx + mcosx – (m + 2)x + 1. Tìm giá trị của m để y’ = 0 có nghiệm?
A. 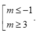
B. m ≥ 2.
C. -1 ≤ m ≤ 3.
D. m ≤ -2.
Chọn A.
y' = (m + 1)cosx – msinx – ( m + 2)
Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)
Điều kiện phương trình có nghiệm là a2 + b2 ≥ c2
⇔ (m + 1)2 + m2 ≥ (m + 2)2 ⇔ m2 – 2m – 3 ≥ 0 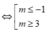
Cho hàm số y = (m + 1)sinx + mcosx - (m+2)x + 1. Tìm giá trị của m để y' = 0 có nghiệm
\(y'=\left(m+1\right)cosx-msinx-\left(m+2\right)\)
\(y'=0\Rightarrow\left(m+1\right)cosx-msinx=m+2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:
\(\left(m+1\right)^2+m^2\ge\left(m+2\right)^2\)
\(\Leftrightarrow m^2-2m-3\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-1\end{matrix}\right.\)
sinx ≠ 0 ⇔ x ≠ k.π
cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên
sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π
cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π
em thắc mắc là tại sao lại những công thức này vậy ạ,:((((((
Vậy thì bạn phải biết đọc đường tròn lượng giác
Mà đừng hỏi mình đọc đường tròn lượng giác thế nào nhé, cái đấy SGK viết rất rõ rồi
sinx ≠ 0 ⇔ x ≠ k.π
cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên
sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π
cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π
em thắc mắc là tại sao lại những công thức này vậy ạ,:((((((
\(\sqrt{\frac{1+sinx}{1-sinx}}-\sqrt{\frac{1-sinx}{1+sinx}}\) các bạn tính giúp mình làm sao ra 1 với ạ
Kết quả rút gọn bằng \(2tanx\) bạn nhé, ko phải ra 1
phương trình2sin5x/2 .sinx/2 -mcosx +1=0 có đúng 7 nghiệm thuộc(-pi/2;2pi). tìm cá giá trị của m
Đề thế này hả bạn: \(2sin\frac{5x}{2}.sin\frac{x}{2}-mcosx+1=0\)
\(\Leftrightarrow cos2x-cos3x-mcosx+1=0\)
\(\Leftrightarrow2cos^2x-1-4cos^3x+3cosx-mcosx+1=0\)
\(\Leftrightarrow cosx\left(4cos^2x-2cosx+m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\4cos^2x-2cosx+m-3=0\left(1\right)\end{matrix}\right.\)
Do \(cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\) có 2 nghiệm thuộc \(\left(-\frac{\pi}{2};2\pi\right)\)
\(\Rightarrow\) Để pt có 7 nghiệm thì (1) có đúng 5 nghiệm thuộc \(\left(-\frac{\pi}{2};2\pi\right)\)
Đặt \(cosx=a\Rightarrow4a^2-2a+m-3=0\) (2)
Dựa vào đường tròn lượng giác, ta thấy để (1) có 5 nghiệm thì (2) có 2 nghiệm phân biệt thỏa mãn: \(-1< a_1\le0< a_2< 1\)
- Với \(m=3\) thay vào pt thấy thỏa mãn
- Với \(m\ne3\)
+ Để pt có 2 nghiệm trái dấu thì: \(4\left(m-3\right)< 0\Rightarrow m< 3\)
+ Để pt có 2 nghiệm thỏa mãn \(-1< a_1< a_2< 1\)
\(\Rightarrow\left\{{}\begin{matrix}4f\left(-1\right)>0\\4f\left(1\right)>0\\-1< \frac{S}{2}< 1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-3\\m>1\\-1< \frac{1}{4}< 1\end{matrix}\right.\) \(\Rightarrow m>1\Rightarrow1< m< 3\)
Vậy \(1< m\le3\)
Khi m ≠ 0 , m ≠ ± 2 phương trình m sin x - 2 m - 2 cos x = m cos x - 2 m - 2 sin x có bao nhiêu nghiệm thuộc đoạn [ 20 π ; 30 π ] ?
A. 10.
B. 9.
C. 20.
D. 18.
tìm m để phương trình mcosx+(m−1)sinx=3−2m có nghiệm
muốn giải bài này nhanh bạn cần biết đến công thức
PT:a.sinx +b.cosx =c có nghiệm khi:\(a^2+b^2\ge c^2\)
ADCT:\(\left(m-1\right)^2+m^2\ge3-2m\)
\(\Leftrightarrow m^2\ge1\)
\(\left[\begin{matrix}m\ge1\\m\le-1\end{matrix}\right.\)
Bài 1: Tìm m để các phương trình sau có nghiệm
a) \((m+2)sinx+mcosx=2\)
b) \(msinx+(m-1)cosx=2m+1\)
c) \((m+2)sin2x+mcos^2x=m-2+msin^2x\)
Bài 2: Tìm m để các phương trình sau vô nghiệm
a) \((2m-1)sinx+(m-1)cosx=m-3\)
b) \(2sinx+cosx=m(sinx-2cosx+3)\)
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
1.
c, \(\left(m+2\right)sin2x+mcos^2x=m-2+msin^2x\)
\(\Leftrightarrow\left(m+2\right)sin2x+m\left(cos^2x-sin^2x\right)=m-2\)
\(\Leftrightarrow\left(m+2\right)sin2x+mcos2x=m-2\)
Phương trình vô nghiệm khi:
\(\left(m+2\right)^2+m^2< \left(m-2\right)^2\)
\(\Leftrightarrow m^2+4m+4+m^2< m^2-4m+4\)
\(\Leftrightarrow m^2+8m< 0\)
\(\Leftrightarrow-8\le m\le0\)