tim x để biểu thức sau có giá trị là số nguyên
12-x/x-5
a) Tim giá trị nguyên của x để biểu thức \(\frac{11}{\sqrt{x}-5}\) nhận giá trị nguyên
b) Tim số nguyên x để B=\(\frac{\sqrt{x}+1}{\sqrt{x}-3}\) có giá trị là số nguyên dương
a) Để \(\frac{11}{\sqrt{x}-5}\)nhận giá trị nguyên thì \(\sqrt{\text{x}}-5\inƯ\left(11\right)\)(DK : \(0\le x\ne25\))
Vì \(\sqrt{\text{x}}-5\ge-5\)nên ta có :
\(\sqrt{x}-5\in\left\{-1;1;11\right\}\)\(\Rightarrow\sqrt{x}\in\left\{4;6;16\right\}\Rightarrow x\in\left\{16;36;256\right\}\)
b) \(B=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)(DK : \(0\le x\ne9\))
Để B nhận giá trị nguyên thì \(\sqrt{x}-3\inƯ\left(4\right)\)
Vì \(\sqrt{\text{x}}-3\ge-3\)nên ta có :
\(\sqrt{\text{x}}-3\in\left\{-2;-1;1;2;4\right\}\)\(\Rightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\Rightarrow x\in\left\{1;4;16;25;49\right\}\)
Tìm giá trị nguyên của \(x\) để giá trị của biểu thức sau có giá trị là số nguyên. \(A=\dfrac{2x^3+x^2+2x+5}{2x+1}\)
\(A=\left(2x+1\right)\left(x^2+1\right)+\dfrac{4}{2x+1}\) (chia đa thức)
Để A nguyên \(\Rightarrow4⋮2x+1\Rightarrow\left(2x+1\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x=\left\{-\dfrac{5}{2};-\dfrac{3}{2};-1;0;\dfrac{1}{2};\dfrac{3}{2}\right\}\)
x thỏa mãn đk đề bài là \(x=\left\{-1;0\right\}\)
1. tim x biết
a, -12(x-5)+7(3-x)=5
b,(x-3)+(x-2)+...+10+11=11
2atim giá trị nhỏ nhất của biểu thức:7-(x-3)^2
b tim giá trị nhỏ nhất cua biểu thức:15+/x-3/
c tim giá trị lớn nhất của biểu thức:21-/x+5/
d tim giá trị lớn nhất của biểu thức:18-(x+3)^2
3a chứng minh n(3n+1)là số chắn
b chứng minh a(a+1)(a-1)chia hết cho 6
1. a, => -12x+60+21-7x = 5
=> 81 - 19x = 5
=> 19x = 81 - 5 = 76
=> x = 76 : 19 = 4
Tk mk nha
(2 điểm) Cho hai biểu thực A= 17 sqrt x+2 v hat aB = (sqrt(x))/(sqrt(x) - 2) + (sqrt(x - 10))/(x ≠4) a) Tính giá trị của biểu thức A khi x = 9 b) rút gọn B c) Tim x nguyên để biểu thúc P = A:B có giá trị là số nguyên
a: Khi x=9 thì \(A=\dfrac{17}{3+2}=\dfrac{17}{5}\)
b: 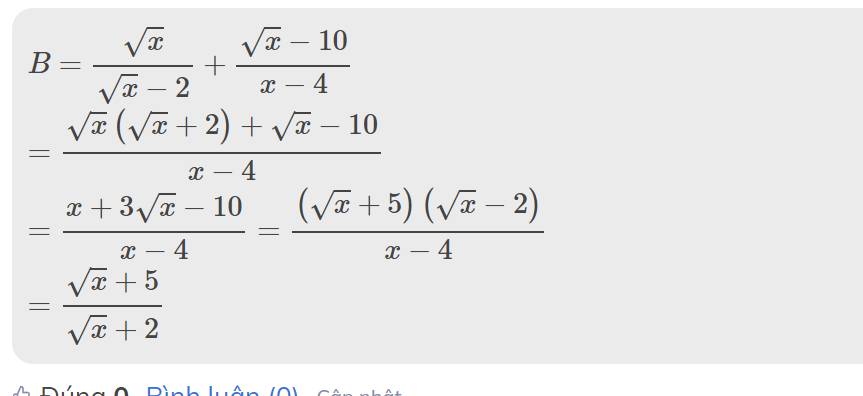
c: P=A:B
\(=\dfrac{17}{\sqrt{x}+2}:\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{17}{\sqrt{x}+5}\)
Để P là số nguyên thì \(17⋮\sqrt{x}+5\)
mà \(\sqrt{x}+5>=5\) với mọi x thỏa mãn ĐKXĐ
nên \(\sqrt{x}+5=17\)
=>x=144
Tính giá trị các số nguyên x để biểu thức sau có giá trị nhỏ nhất A=1/x-3 B=7-x/x-5 C=5x-19/x-4
\(A=\dfrac{1}{x-3}\Rightarrow x-3\inƯ\left(1\right)=\left\{\pm1\right\}\)
| x-3 | 1 | -1 |
| x | 4 | 2 |
\(B=\dfrac{7-x}{x-5}=\dfrac{-\left(x-5-2\right)}{x-5}=\dfrac{-\left(x-5\right)+2}{x-5}\Rightarrow x-5\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x-5 | 1 | -1 | 2 | -2 |
| x | 6 | 4 | 7 | 3 |
\(C=\dfrac{5x-19}{x-5}=\dfrac{5\left(x-5\right)+6}{x-5}\Rightarrow x-5\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| x-5 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| x | 6 | 4 | 7 | 3 | 8 | 2 | 11 | -1 |
Cho biểu thức:A=\(\dfrac{2x-1}{x+2}\)
a) Tìm số nguyên x để biểu thức A là phân số
b)Tìm các số nguyên x để biểu thức A có giá trị là 1 số nguyên
c)Tìm các số nguyên x để biểu thức A đạt giá trị lớn nhất,giá trị nhỏ nhất
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
Tim \( x \) để biểu thức sau đạt giá trị nhỏ nhất:
\[
A=|x+1|+|x+2|+|x+3|+\ldots+|x+8|
\]
Tìm giá trị số tự nhiên a để biểu thức sau có giá trị lớn nhất,giá trị nhỏ nhất là bao nhiêu
C= (a-30) x (a-29) x...x (a-1)
Tìm giá trị nguyên x để biểu thức sau có giá trị nhỏ nhất A = \(\dfrac{7-x}{x-5}\)
Tham khảo:
Tìm giá trị nguyên của x để biểu thức B=(7-x)/(x-5) có giá trị nhỏ nhất - Lê Nhi
\(A=\dfrac{-x+5+2}{x-5}=-1+\dfrac{2}{x-5}\)
Để A đạt min thì \(\left\{{}\begin{matrix}A\in Z\\x\in Z\end{matrix}\right.\)
\(\Rightarrow x-5\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Rightarrow x\in\left\{3;4;6;7\right\}\)
Với \(x=3\Rightarrow A=-2\)
Với \(x=4\Rightarrow A=-3\)
Với \(x=6\Rightarrow A=1\)
Với \(x=7\Rightarrow A=0\)
Vậy \(A_{min}=-3\Rightarrow x=4\)