x6-2x5+9x4-12x3+28x2-8x+20=0

Những câu hỏi liên quan
mình cần các bạn giải 2 bài sau
59:57+12x3+70
520:(515x6+515x19)
a) 5^9 : 5^7 + 12 . 3 + 7^0 = 5^2 + 36 + 1 = 25 +36 + 1 = 61 + 1 = 62.
b) 5^20 : (5^15 . 6 + 5^15 . 19) = 5^20 : [5^15 . (6+19)] = 5^20 : [5^15 . 25] = 5^20 : [5^15 . 5^2] = 5^20 : 5^17 = 5^3 = 125.
Đúng 0
Bình luận (0)
Mình mới tham gia Online math nên điểm còn ít lắm, bạn k cho mình nha!
Đúng 0
Bình luận (0)
(-0.2)^2x5-(8^2x9^5)/3^9x4^3
\(=0.04\cdot5-\dfrac{2^6\cdot3^{10}}{3^9\cdot2^6}=0.2-3=-2.8\)
Đúng 1
Bình luận (0)
Tìm thương của mỗi phép chia sau:
a) 12x3 : 4x
b) (-2x4) : x4
c) 2x5 : 5x2
a) 12x3 : 4x = (12:4) . (x3 : x) = 3.x2
b) (-2x4 ) : x4 = [(-2) : 1] . (x4 : x4) = -2
c) 2x5 : 5x2 = (2:5) . (x5 : x2) = \(\frac{2}{5}\)x3
Đúng 1
Bình luận (0)
Tìm x biết:a)
x
6
+ 2
x
3
+1 0; b) x(x - 5) 4x - 20;c)
x
4
-2
x
2
8-4
x
2
; d) (
x
3
-
x
2
) - 4
x
2
+ 8x-4 0.
Đọc tiếp
Tìm x biết:
a) x 6 + 2 x 3 +1 = 0; b) x(x - 5) = 4x - 20;
c) x 4 -2 x 2 =8-4 x 2 ; d) ( x 3 - x 2 ) - 4 x 2 + 8x-4 = 0.
a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.
Đúng 0
Bình luận (0)
(x6 - 2x5 + 2x4 + 6x3 - 4x2) : 6x2
bạn chia đa thức 1 biến đã sắp xếp nha
Đúng 1
Bình luận (1)
Cho các đa thức:
P(x)=−12x2+34x4−12x3−14x+2x5 ; Q(x)=0,5x2+12x4−2x3−14−2x5
a) Sắp xếp các hạng tử của các đa thức theo lũy thừa giảm dần của biến
b) Tính P(x) + Q(x) và P(x) – Q(x)
c) x = 0 là nghiệm của đa thức P(x) hay Q(x)
Giúp mình luôn với, mình đang cần để làm bài
* Có mũ hết đúng chứ? :)
\(a)\)
\(P\left(x\right)=-12x^2+34x^4-12x^3-14x+2x^5\)
\(=2x^5+34x^4-12x^3-12x^2-14x\)
\(Q\left(x\right)=0,5x^2+12x^4-2x^3-14-2x^5\)
\(=-2x^5+12x^4-2x^3+0,5x^2-14\)
c, Thay x = 0 vào P(x) ta được :
\(P\left(x\right)=0+0-0-0+0=0\)* đúng *
Vậy x = 0 là nghiệm của đa thức P(x)
Thay x = 0 vaò Q(x) ta được
\(Q\left(x\right)=0+0-0-14-0=-14\)
Vậy x = 0 ko là nghiệm của đa thức Q(x)
\(b)\)
\(P\left(x\right)+Q\left(x\right)\)\(\rightarrow\left(2x^5+34x^4-12x^3-12x^2-14x\right)+\left(-2x^5+12x^4-2x^3+0,5x^2-14\right)\)
\(\rightarrow2x^5+34x^4-12x^3-12x^2-14x-2x^5+12x^4-2x^3+0,5x^2-14\)
\(\rightarrow\left(2x^5-2x^5\right)+\left(34x^4+12x^4\right)+\left(-12x^3-2x^3\right)+\left(-12x^2+0,5x^2\right)-14x-14\)
\(\rightarrow46x^4-14x^3-\frac{23}{2}x^2-14x-14\)
\(P\left(x\right)-Q\left(x\right)\)
\(\rightarrow\left(2x^5+34x^4-12x^3-12x^2-14x\right)-\left(-2x^5+12x^4-2x^3+0,5x^2-14\right)\)
\(\rightarrow2x^5+34x^4-12x^3-12x^2-14x+2x^5-12x^4+2x^3-0,5x^2+14\)
\(\rightarrow\left(2x^5+2x^5\right)+\left(34x^4-12x^4\right)+\left(-12x^3+2x^3\right)+\left(-12x^2-0,5x^2\right)-14x+14\)
\(\rightarrow4x^5+22x^4-10x^3-\frac{25}{2}x^2-14x+14\)
Cho hai đa thức A(x) x6 - 2x5 + 4x4 + 5x3 - 4x + 7 + 5x4 B(x) -x6 - 2x5 + 9x4 - 3x3 + 2x - 2x3 - 7 a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến b) Tính A(x) + B(x) và A(x) - B(x)
Đọc tiếp
Cho hai đa thức A(x) = x6 - 2x5 + 4x4 + 5x3 - 4x + 7 + 5x4 B(x) = -x6 - 2x5 + 9x4 - 3x3 + 2x - 2x3 - 7 a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến b) Tính A(x) + B(x) và A(x) - B(x)
a)
A(x) = \(x^6-2x^5+9x^4+5x^3-4x+7\)
B(x) = \(-x^6-2x^5+9x^4-5x^3+2x-7\)
b)
A(x)+B(x) = \(-4x^5+18x^4-2x\)
A(x)-B(x) = \(2x^6+10x^3-6x+14\)
Đúng 0
Bình luận (0)
Cho hai đa thức:
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1.
Tính P(x) + Q(x) và P(x) – Q(x).
Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
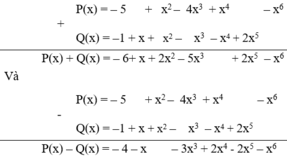
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6
Đúng 0
Bình luận (0)
Cho các sơ đồ phản ứng theo đúng tỉ lệ mol: (a) X + 2NaOH X1 + 2X2 (b) X1 + H2SO4 X3 + Na2SO4 (c) nX3 + nX4 poli(etylen terephtalat) + 2nH2O (d) X2 + CO X5 (e) X4 + 2X5 X6 + 2H2O Cho biết, X là este có công thức phân tử C10H10O4; X1, X2, X3, X4, X5, X6 là các hợp chất hữu cơ khác nhau. Phân tử khối của X6 và X2 lần lượt là A. 164 và 46 B. 146 và 46 C. 164 và 32 D. 146 và 32
Đọc tiếp
Cho các sơ đồ phản ứng theo đúng tỉ lệ mol:
(a) X + 2NaOH X1 + 2X2
(b) X1 + H2SO4 X3 + Na2SO4
(c) nX3 + nX4 poli(etylen terephtalat) + 2nH2O
(d) X2 + CO X5
(e) X4 + 2X5 X6 + 2H2O
Cho biết, X là este có công thức phân tử C10H10O4; X1, X2, X3, X4, X5, X6 là các hợp chất hữu cơ khác nhau. Phân tử khối của X6 và X2 lần lượt là
A. 164 và 46
B. 146 và 46
C. 164 và 32
D. 146 và 32
Chọn D.
(c) p-HOOC-C6H4-COONa (X3) + C2H4(OH)2 (X4) → x t , t ∘ poli(etilen-terephtalat) + 2nH2O.
(b) p-NaOOC-C6H4-COONa (X1) + H2SO4 → p-HOOC-C6H4-COOH (X3) + Na2SO4.
(d) CH3OH (X1) + CO → CH3COOH (X5).
(a) p-CH3-OOC-C6H4-COO-CH3 (X) + 2NaOH → t ∘ p-NaOOC-C6H4-COONa + 2CH3OH (X2).
(e) C2H4(OH)2 + 2CH3COOH ⇄ t ∘ H 2 S O 4 (CH3COO)2C2H4 (X6) + 2H2O
Đúng 0
Bình luận (0)
Cho các sơ đồ phản ứng theo đúng tỉ lệ mol: (a) X + 2NaOH
→
t
°
X1 + 2X2 (b) X1 + H2SO4
→
X3 + Na2SO4 (c) nX3 + nX4
→
t
°
poli(etylen terephtalat) + 2nH2O (d) X2 + CO
→
t
°
,...
Đọc tiếp
Cho các sơ đồ phản ứng theo đúng tỉ lệ mol:
(a) X + 2NaOH → t ° X1 + 2X2 (b) X1 + H2SO4 → X3 + Na2SO4
(c) nX3 + nX4 → t ° poli(etylen terephtalat) + 2nH2O (d) X2 + CO → t ° , x t X5
(e) X4 + 2X5 ⇆ H 2 S O 4 đ , t ° X6 + 2H2O
Cho biết: X là este có công thức phân tử C10H10O4; X1, X2, X3, X4, X5, X6 là các hợp chất hữu cơ khác nhau. Phân tử khối của X6 là
A. 146.
B. 104.
C. 118.
D. 132.
























