cho hàm số: \(y=-x+3m\) ; với m là tham số.
Tính theo m tọa độ các giao điểm A; B của đồ thị hàm đồ thị hàm số với Ox và Oy. Xác định giá trị của m để AB=6
Cho hàm số y = x 3 + 3 x 2 + 3 m − 1 x − 3 m − 1 với m là tham số thực. Tìm m để hàm số
đạt cực trị tại x = -1
A. m = 4
B. m = 2
C. m = -2
D. m = ∅
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Cho hàm số y=(3m-6)x+3 tìm m để a) hàm số nghịch biến
Để hàm số nghịch biến thì
3m - 6 < 0
=> m < 2
Để hàm số nghịch biến thì 3m-6<0
hay m<2
Câu 2: Cho hàm số y = ( 3m-1)x + m +2 . Tìm tham số m để đồ thị hàm số cắt trục tung tại điểm có tung độ là −3.
Câu 3: Cho hàm số y = 2mx-3m+2 . Tìm tham số m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 2
Câu 2:
Thay x=0 và y=-3 vào (d), ta được:
m+2=-3
hay m=-5
Cho hàm số y = ( 3 m – 2 ) x + 5 m . Tìm m để hàm số nhận giá trị là 2 khi x = − 1
A. m = 0
B. m = 1
C. m = 2
D. m = − 1
Thay x = − 1 ; y = 2 v à o y = ( 3 m – 2 ) x + 5 m t a đ ư ợ c 2 = ( 3 m – 2 ) . ( − 1 ) + 5 m
⇔ 2 m = 0 ⇔ m = 0
Đáp án cần chọn là: A
cho hàm số y=f(x)=(3m-2)x a) tìm m biết đồ thị hàm số đi qua điểm M(1,4)
Do đồ thị hàm số đi qua M(1;4) nên:
\(\left(3m-2\right).1=4\)
\(\Rightarrow3m-2=4\)
\(\Rightarrow3m=6\)
\(\Rightarrow m=2\)
cho hàm số y=f(x)=(3m-2)x a) tìm m biết đồ thị hàm số đi qua điểm M(1,4)
đồ thị hàm số y=f(x)=(3m-2)x đi qua điểm M(1,4) thì:
\(4=\left(3m-2\right).1\\
\Rightarrow3m-2=4\\
\Rightarrow3m=6\\
\Rightarrow m=2\)
cho hàm số y = (2 - 3m)x + 2m - 5
tìm điểm cố định ( bất động) của đồ thị hàm số
\(y=\left(2-3m\right)x+2m-5\\ \Rightarrow m\left(3x+2\right)+2x-y-5=0\)
Để hàm số cố định thì \(\left\{{}\begin{matrix}3x+2=0\\2x-y-5=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=-\dfrac{19}{3}\end{matrix}\right.\)
Điểm cố định là: \(\left(-\dfrac{2}{3};-\dfrac{19}{3}\right)\)
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau
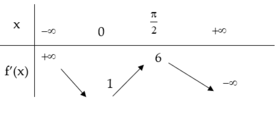 Bất phương trình
f
x
>
2
cos
x
+
3
m
đúng với mọi
x
∈
0
;
π
2
khi
Bất phương trình
f
x
>
2
cos
x
+
3
m
đúng với mọi
x
∈
0
;
π
2
khi
A. m ≤ 1 3 f 0 - 2
B. m < 1 3 f 0 - 2
C. m ≤ 1 3 f π 2 - 1
D. m < 1 3 f π 2 - 1
Cho hàm số y = ( 4 – 3 m ) x 2 , m ≠ 4 3 . Tìm m để hàm số đồng biến với mọi x < 0
A. m > 4 3
B. m < - 4 3
C. m < 4 3
D. m > - 4 3
Để hàm số đồng biến với mọi x > 0 thì a > 0
nên 4 – 3m > 0 ⇔ 4 > 3m
⇔ 3m < 4 ⇔ m < 4 3
Vậy m < 4 3 thỏa mãn điều kiện đề bài
Đáp án cần chọn là: C