tìm 2 số thực m, n để có {x \(\epsilon\)R/ x2 -mx+n=0} ={1;2}
tìm 2 số thực m, n để có {x \(\varepsilon\)R/ x3 -mx2 +nx -2 =0}= {1; 2}
Những câu hỏi liên quan
Tìm các số thực m , n để có {x thuộc R/ x^2-mx+n=0} ={1,2}
Tìm m để (m + 1) x 2 + mx + m < 0, ∀x ∈ R?
A. m < -1
B. m > -1
C. m < - 4 3
D. m > 4 3
Đáp án C
Bất phương trình (m + 1) x 2 + mx + m < 0, ∀x ∈ R khi và chỉ khi:
Đúng 0
Bình luận (0)
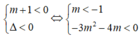
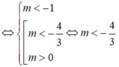
Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R
Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
2
(
x
2
+
m
x
)
-
2
(
2
x
2
+
2
m
x
+
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 ( x 2 + m x ) - 2 ( 2 x 2 + 2 m x + m ) = x 2 +mx+m có nghiệm thực
A. ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
B. ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ ) .
C. ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ ) .
D. ( - ∞ ; - 4 ] ∪ [ 0 ; + ∞ ) .
Cho A {
x
∈
R
|
|
m
x
−
3
|
m
x
−
3
}
,
B
{
x
∈
R
|
x
2
−
4
0
}. Tìm m để B∖AB A.
−...
Đọc tiếp
Cho A ={ x ∈ R | | m x − 3 | = m x − 3 } , B = { x ∈ R | x 2 − 4 = 0 }. Tìm m để B∖A=B
A. − 3 2 ≤ m ≤ 3 2
B. 0 < m < 3 2 hoặc − 3 2 < m < 0
C. − 3 2 < m < 3 2
D. m ≥ − 3 2
Tìm số giá trị nguyên của tham số thực m để hàm số
y
x
2
+
m
x
+
6
3
+
2
xác định trên R A. 9 B. 5 C. 10 D. 6
Đọc tiếp
Tìm số giá trị nguyên của tham số thực m để hàm số y = x 2 + m x + 6 3 + 2 xác định trên R
A. 9
B. 5
C. 10
D. 6
cho phương trinh \(x^2+mx+2n+1=\)0 ( x là ẩn:m,n là tham số ). Xác định m và n để phương trình có 2 nghiệm là x1=1; x2=-2
Cho phương trình x^2 - mx +m -1 =0 với m là tham số tìm m để phương trình có hai nghiệm phân biệt x1 x2 thỏa mãn:
a) x1 - x2 = 5
b) 1/x1 +1/x2-2 =1/2
c) |x1|=2|x2|
a: \(\text{Δ}=\left(-m\right)^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
để phương trình có hai nghiệm phân biệt thì m-2<>0
hay m<>2
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1-x_2=5\\x_1x_2=m-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x_1=m+5\\x_2=x_1-5\\x_1x_2=m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+5}{2}\\x_2=\dfrac{m+5}{2}-5=\dfrac{m-5}{2}\\x_1x_2=m-1\end{matrix}\right.\)
\(\Leftrightarrow m^2-25=4m-4\)
\(\Leftrightarrow m^2-4m-21=0\)
=>(m-7)(m+3)=0
=>m=7 hoặc m=-3
Đúng 1
Bình luận (0)
Tìm m để phương trình: \(mx^2-2\left(m+1\right)x+m+5=0\) có 2 nghiệm x1,x2 thỏa mãn x1<0<x2<2
Lời giải:
Để pt có 2 nghiệm thì:
\(\left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-m(m+5)=1-3m\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ m\leq\frac{1}{3}\end{matrix}\right.(1)\)
Áp dụng định lý Viet:
\(\left\{\begin{matrix} x_1+x_2=\frac{2(m+1)}{m}\\ x_1x_2=\frac{m+5}{m}\end{matrix}\right.\)
Để $x_1< 0< x_2$
$\Leftrightarrow x_1x_2< 0$
$\Leftrightarrow \frac{m+5}{m}< 0$
$\Leftrightarrow -5< m< 0(2)$
$x_1< x_2< 2$
\(\Leftrightarrow \left\{\begin{matrix} (x_1-2)(x_2-2)>0\\ x_1+x_2<4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_1x_2-2(x_1+x_2)+4>0\\ x_1+x_2<4\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{m+1}{m}>0\\ \frac{1-m}{m}< 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m>1\\ m< -1\end{matrix}\right.(3)\)
Từ $(1);(2);(3)$ suy ra $-5< m< -1$
Đúng 1
Bình luận (0)