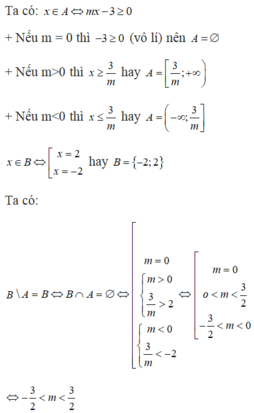Các câu hỏi tương tự
cho A={x\(\in\)R| |mx-3|=mx-3}, B={x\(\in\)R| \(x^2\)-4=0}. Tìm m để B\A=B
A= { x ∈ R | |mx - 3 | = mx -3} , B= { x ∈ R | x\(^2\) - 4 = 0 } . Tìm m để B \ A
Tìm tất cả các giá trị nguyên của m để các tập hợp sau là tập hợp rỗng.
a) A = {x ∈ R | x < m + 3 và x > 4m + 3}.
b) B = {x ∈ R | x^2 − 2x + m + 9 = 0}
Cho hai tập hợp \(A=\left(0;+\infty\right)\) và \(B=\left\{x\in R|mx^2-4x+m-3=0\right\}\). Tìm m để B có đúng 2 tập hợp con và \(B\subset A\)
Phương trình
(
m
+
1
)
x
2
-
3
(
m
-
1
)
x
+
2
0
có một nghiệm gấp đôi nghiệm kia thì giá trị của tham số m là: A. m 1 B. m -1 C. m 0 hoặc m 3 D. m 2
Đọc tiếp
Phương trình
( m + 1 ) x 2 - 3 ( m - 1 ) x + 2 = 0
có một nghiệm gấp đôi nghiệm kia thì giá trị của tham số m là:
A. m = 1 B. m = -1
C. m = 0 hoặc m = 3 D. m = 2
Câu 1.Tìm m để phương trình sau có nghiệm (m - 1)x - 2 0.A. m1 B. m - 1 C. m0 D. m≠ 1Câu 2. Phương trình left(m^2-4right)x3m+6 có nghiệm duy nhất khi và chỉ khiA. mnepm2;mne-3 B. mne-2 C. mne2 D. mnepm2
Đọc tiếp
Câu 1.Tìm m để phương trình sau có nghiệm (m - 1)x - 2 = 0.
A. m=1 B. m= - 1 C. m=0 D. m≠ 1
Câu 2. Phương trình \(\left(m^2-4\right)x=3m+6\) có nghiệm duy nhất khi và chỉ khi
A. \(m\ne\pm2;m\ne-3\) B. \(m\ne-2\) C. \(m\ne2\) D. \(m\ne\pm2\)
Bài 1: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm trái dấu:a,left(m^2-1right)x^2+left(m+3right)x+left(m^2+mright)0b,x^2-left(m^2+m-2right)x+m^2+m-50Bài 2: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm dương phân biệt:a,x^2-2x+m^2+m+30b,left(m^2+m+1right)x^2+left(2m-3right)x+m-50c,x^2-6mx+2-2m+9m^20
Đọc tiếp
Bài 1: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm trái dấu:
\(a,\left(m^2-1\right)x^2+\left(m+3\right)x+\left(m^2+m\right)=0\)
\(b,x^2-\left(m^2+m-2\right)x+m^2+m-5=0\)
Bài 2: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm dương phân biệt:
\(a,x^2-2x+m^2+m+3=0\)
\(b,\left(m^2+m+1\right)x^2+\left(2m-3\right)x+m-5=0\)
\(c,x^2-6mx+2-2m+9m^2=0\)
Tìm các giá trị của tham số m để phương trình
m
x
2
+
2
(
2
m
-
1
)
x
+
m
+
2
0
vô nghiệm A.
3
-
6
3
m...
Đọc tiếp
Tìm các giá trị của tham số m để phương trình m x 2 + 2 ( 2 m - 1 ) x + m + 2 = 0 vô nghiệm
A. 3 - 6 3 < m < 3 + 6 3
B. Không tồn tại m
C. m < 1/12
D. m ≠ 0; m < 1/12
Tìm m để phương trình
x
2
+
2
(
m
+
1
)
x
+
2
(
m
+
6
)
0
có hai nghiệm
x
1
,
x
2
mà
x
1...
Đọc tiếp
Tìm m để phương trình x 2 + 2 ( m + 1 ) x + 2 ( m + 6 ) = 0 có hai nghiệm x 1 , x 2 mà x 1 + x 2 = 4
A. m = 1
B. m = -3
C. m = -2
D. Không tồn tại m