Đáp án C
Bất phương trình (m + 1) x 2 + mx + m < 0, ∀x ∈ R khi và chỉ khi:
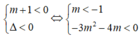
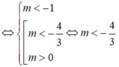
Đáp án C
Bất phương trình (m + 1) x 2 + mx + m < 0, ∀x ∈ R khi và chỉ khi:
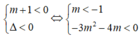
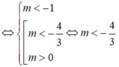
cho A={x\(\in\)R| |mx-3|=mx-3}, B={x\(\in\)R| \(x^2\)-4=0}. Tìm m để B\A=B
Cho A ={ x ∈ R | | m x − 3 | = m x − 3 } , B = { x ∈ R | x 2 − 4 = 0 }. Tìm m để B∖A=B
A. − 3 2 ≤ m ≤ 3 2
B. 0 < m < 3 2 hoặc − 3 2 < m < 0
C. − 3 2 < m < 3 2
D. m ≥ − 3 2
A= { x ∈ R | |mx - 3 | = mx -3} , B= { x ∈ R | x\(^2\) - 4 = 0 } . Tìm m để B \ A
1. Có bao nhiêu \(m\in Z\) \(\in\left[-30;40\right]\) để bpt sau đúng \(\forall x\in R\)
\(a.\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)\ge m\)
b.\(b.\left(x^2-2x+4\right)\left(x^2+3x+4\right)\ge mx^2\)
2. Tìm m để pt
\(\left(m+3\right)x-2\sqrt{x^2-1}+m-3=0\) có nghiệm \(x\ge1\)
Câu 1.Tìm m để phương trình sau có nghiệm (m - 1)x - 2 = 0.
A. m=1 B. m= - 1 C. m=0 D. m≠ 1
Câu 2. Phương trình \(\left(m^2-4\right)x=3m+6\) có nghiệm duy nhất khi và chỉ khi
A. \(m\ne\pm2;m\ne-3\) B. \(m\ne-2\) C. \(m\ne2\) D. \(m\ne\pm2\)
Tìm m để phương trình x 2 + 2 ( m + 1 ) x + 2 ( m + 6 ) = 0 có hai nghiệm x 1 , x 2 mà x 1 + x 2 = 4
A. m = 1
B. m = -3
C. m = -2
D. Không tồn tại m
1/ tìm tham số thực m để tồn tại x thỏa mãn f(x) = m^2x + 3 - ( mx + 4 ) âm. 2/ tìm tất cả các giá trị của m để f (x) = m( x-m ) - ( x - 1 ) không âm với mọi x thuộc ( - vô cực , m+1)
1/ Tìm các giá trị của tham số m để bpt ( m-1) x^2- ( m-1) x+1>0 nghiệm đúng vs mọi giá trị của x. 2/ Tìm giá trị của tham số m để pt x^2 - ( m-2) x+m^2 -4m=0 có 2 nghiệm trái dấu. 3/ Tìm giá trị của tham số m để pt x^2 -mx+1=0 có 2 nghiệm phân biệt.
cho pt x^4 - 2x^3 - mx^2 + 2x +1 = 0. tìm m để pt có 4 nghiệm