Số giá trị \(m\in Z\) và \(m\in\left[-10;10\right]\) để hàm số \(y=\frac{m\cos x+m-1}{3+\sin x+\cos x}< 1\forall x\in R\) ?

Những câu hỏi liên quan
Cho a là số thực dương và đặt
\(M_0=\left\{z\in C^+,\left|z+\frac{1}{z}\right|=a\right\}\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của \(\left|z\right|\) khi \(z\in M_0\)
\(a^2=\left|z+\frac{1}{z}\right|^2=\left(z+\frac{1}{z}\right)\left(\overline{z}+\frac{1}{z}\right)=\left|z\right|^2+\frac{z^2+\overline{z}^2}{\left|z\right|^2}+\frac{1}{\left|z\right|^2}\)
\(=\frac{\left|z\right|^4+\left(z+\overline{z}\right)^2-2\left|z\right|^2+1}{\left|z\right|^2}\)
Do đó :
\(\left|z\right|^4-\left|z\right|^2\left(a^2+2\right)+1=-\left(z+\overline{z}\right)^2\le0\)
\(\Rightarrow\left|z\right|^2\in\left[\frac{a^2+2-\sqrt{a^4+4a^2}}{2};\frac{a^2+2+\sqrt{a^4+4a^2}}{2}\right]\)
\(\Rightarrow\left|z\right|\in\left[\frac{-a+\sqrt{a^4+4a^2}}{2};\frac{a+\sqrt{a^4+4a^2}}{2}\right]\)
max \(\left|z\right|=\frac{a+\sqrt{a^4+4a^2}}{2}\)
min \(\left|z\right|=;\frac{a+\sqrt{a^4+4a^2}}{2}\)
\(\Leftrightarrow z\in M,z=-\overline{z}\)
Đúng 0
Bình luận (0)
cho tập \(Â=\left\{x\in R|2x-1< 5\right\},B=\left\{x\in Z|-1\le x\le5\right\}\)
và C là tập giá trị hàm: y=x^2-2x+m trên \([-1;1)\)
a, tìm \(A\cap B\)
b, tìm m để \(C\subset A\)
\(a,\)\(A=\left\{x\in R|x< 3\right\}\Rightarrow A=\left(\text{ -∞;3}\right)\)
\(B=\left\{-1;0;1;2;3;4;5\right\}\)
\(\Rightarrow A\cap B=\left\{-1;0;1;2\right\}\)
\(b,x=-1\Rightarrow y=1-2\left(-1\right)+m=m+3\)
\(x=1\Rightarrow y=1-2+m=m-1\)
\(\Rightarrow C=(m-1;m+3]\subset A\)
\(\Rightarrow C\subset A\Leftrightarrow m+3< 3\Leftrightarrow m< 0\)
Đúng 2
Bình luận (0)
Cho M=\(\frac{4n+3}{n-1}\left(n\in Z,n\ne1\right)\)tìm n để M có giá trị là một số nguyên
Cho x , y , z \(\in Z\)thỏa : \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z}\). Hãy tính giá trị biểu thức :
\(M=\frac{3}{4}+\left(x^8-y^8\right)\left(y^9+z^9\right)\left(z^{10}-x^{10}\right)\)
tự suy nghĩ nhé bn o0o I am a studious person o0o,chỉ cần ngồi quy đồng sau làm từng bước là được nhaaaaaaaaa :)) ^_^
Đúng 0
Bình luận (0)
Hãy tìm tất cả các h/s f(x) x/đ ; liên tục trên R ; lấy giá trị trong R và t/m các đ/k : \(f\left(x-y\right)f\left(y-z\right)f\left(z-x\right)+8=0\) \(\forall x;y;z\in R\)
Gọi M là giá trị lớn nhất của biểu thức \(S=\sin x+\sin y+\sin\left(3x+y\right)-2\sin\left(2x+y\right).\cos x\) , \(\forall x\in\left(0,2\pi\right),\forall y\in\left(0,2\pi\right)\) . Biết \(M=\dfrac{a\sqrt{b}}{c}\) (Với a,b,c \(\in Z^+,\dfrac{a}{c}\) là phân số tối giản, b < 12). Tính \(P=a+b-c\)
\(S=sinx+siny+sin\left(3x+y\right)-sin\left(3x+y\right)-sin\left(x+y\right)\)
\(=sinx+siny-sin\left(x+y\right)\)
\(S^2=\left(sinx+siny-sin\left(x+y\right)\right)^2\le3\left(sin^2x+sin^2y+sin^2\left(x+y\right)\right)\)
\(S^2\le3\left(1-\dfrac{1}{2}\left(cos2x+cos2y\right)+sin^2\left(x+y\right)\right)\)
\(S^2\le3\left[1-cos\left(x+y\right)cos\left(x-y\right)+1-cos^2\left(x-y\right)\right]\)
\(S^2\le3\left[2+\dfrac{1}{4}cos^2\left(x+y\right)-\left[cos\left(x-y\right)-\dfrac{1}{2}cos\left(x+y\right)\right]^2\right]\le3\left[2+\dfrac{1}{4}cos^2\left(x+y\right)\right]\)
\(S^2\le3\left(2+\dfrac{1}{4}\right)=\dfrac{27}{4}\)
\(\Rightarrow S\le\dfrac{3\sqrt{3}}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=3\\c=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho số phức z thỏa mãn left|z-3-4iright|sqrt{5}. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức Pleft|z+2right|^2-left|z-iright|^2. Môđun của số phức wM+mi là?Giải thích cho mình dòng bôi vàng ở dưới ạ, mình cảm ơn nhiều ♥
Đọc tiếp
Cho số phức \(z\) thỏa mãn \(\left|z-3-4i\right|=\sqrt{5}\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=\left|z+2\right|^2-\left|z-i\right|^2\). Môđun của số phức \(w=M+mi\) là?
Giải thích cho mình dòng bôi vàng ở dưới ạ, mình cảm ơn nhiều ♥

Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)
Đúng 1
Bình luận (2)
Cho hàm số fleft(xright)left|x^2-2x+mright| với minleft[-2018;2018right]. Gọi M là giá trị nhỏ nhất của hàm số fleft(x+dfrac{1}{x}right) trên tập Rbackslashleft{0right}. Số giá trị m nguyên để Mge2 là bao nhiêu?
Đọc tiếp
Cho hàm số \(f\left(x\right)=\left|x^2-2x+m\right|\) với \(m\in\left[-2018;2018\right]\). Gọi \(M\) là giá trị nhỏ nhất của hàm số \(f\left(x+\dfrac{1}{x}\right)\) trên tập \(R\backslash\left\{0\right\}\). Số giá trị \(m\) nguyên để \(M\ge2\) là bao nhiêu?
Dùng đồ thị hàm số, hãy cho biết:a) Với mỗi m in left[ { - 1;1} right], có bao nhiêu giá trị alpha in left[ { - frac{pi }{2};frac{pi }{2}} right] sao cho sin alpha mb) Với mỗi m in left[ { - 1;1} right], có bao nhiêu giá trị alpha in left[ {0;pi } right] sao cho cos alpha mc) Với mỗi m in mathbb{R}, có bao nhiêu giá trị alpha in left[ { - frac{pi }{2};frac{pi }{2}} right] sao cho tan alpha md) Với mỗi m in mathbb{R}, có bao nhiêu giá trị alpha in left[ {0;pi } right] sa...
Đọc tiếp
Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
a) Đồ thị hàm số:
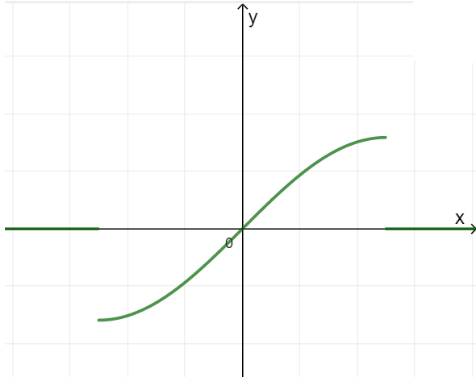
- Với mỗi \(m \in \left[ { - 1;1} \right]\) chỉ có 1 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Đồ thị hàm số:
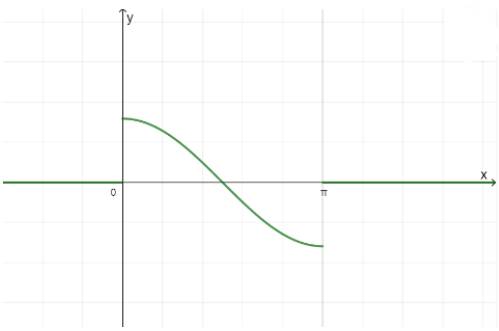
- Với mỗi \(m \in \left[ { - 1;1} \right]\) có 1 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Đồ thị hàm số:
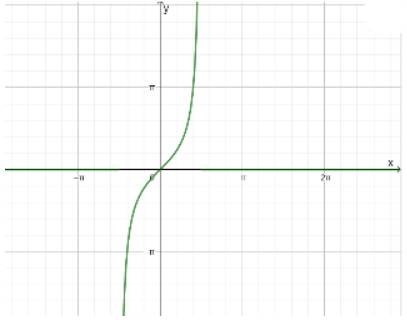
- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Đồ thị hàm số:

- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
Đúng 0
Bình luận (0)
Cho 2 tập hợp \(M=\left\{x\in R|x\le4\right\}\)và \(N=[m+1;10)\), với m là tham số. Tìm giá trị của m để M giao N là một đoạn có độ dài bằng 10.




















