trong mặt phẳng Oxy cho ba điểm A(0;4), B(3;4), C(3;0)
a viết phương trình đường tròn (C) đi qua ba điểm A,B,C
b viết phương trình đường tròn (C) tâm C, tiếp xúc đường thẳng (d) 3x+4y-5=0
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho
M
A
→
+
M
B
→
+
M
C
→
0
→
.
A. M (-2; 0) B. M(2; 0) C. M(- 4; 0) D. M(- 5; 0)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
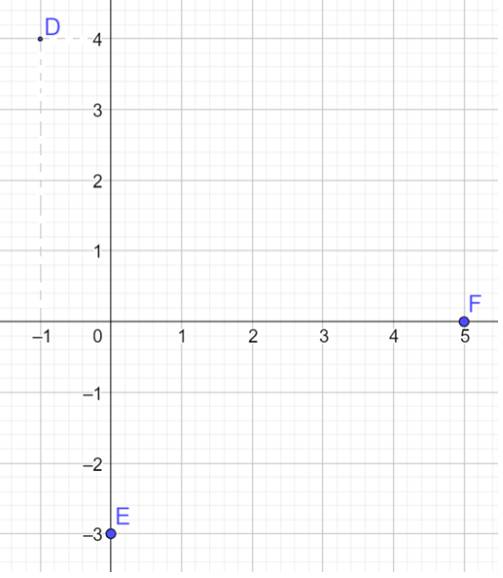
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
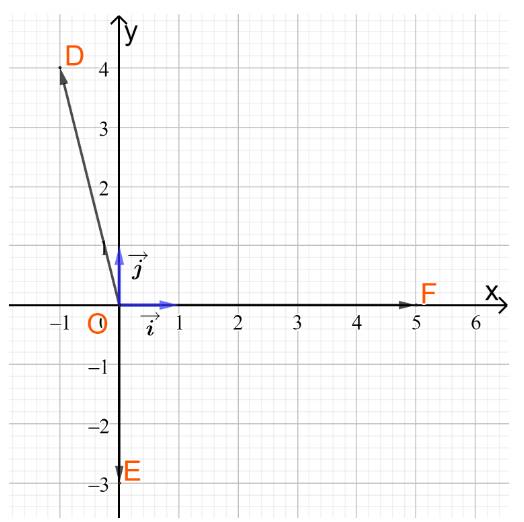
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Đúng 0
Bình luận (0)
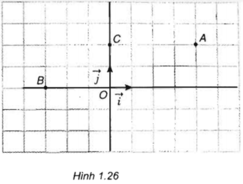
Câu hỏi 3 trang 24: Tìm tọa độ của các điểm A, B, C trong hình 1.26. Cho ba điểm D(-2; 3), E(0; -4), F(3; 0). Hãy vẽ các điểm D, E, F trên mặt phẳng Oxy.
Trong mặt phẳng tọa độ oxy, cho ba điểm A(1 ;0) B(2,-1) C(1,1). Phương trình chính tắc đường thẳng (d) đi qua A và song song với BC
VTCP là (-1;2)
Phương trình chính tắc là: \(\dfrac{x-1}{-1}=\dfrac{y-0}{2}=\dfrac{y}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho bà điểm :
A( 2; -1 ) ; B( -1 ; 5 ) ; C(0 ; 3 )
Chứng minh ba điểm A, B, C thẳng hàng.
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d cắt hai trục Ox và Oy lần lượt tại 2 điểm A(a;0) và
B
0
;
b
a
≠
0
,
b
≠
0
.
Viết phương trình đường thẳng d. A.
d
:
x
a
+
y...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d cắt hai trục Ox và Oy lần lượt tại 2 điểm A(a;0) và B 0 ; b a ≠ 0 , b ≠ 0 . Viết phương trình đường thẳng d.
A. d : x a + y b = 0
B. d : x a − y b = 1
C. d : x a + y b = 1
D. d : x b + y a = 0
Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
Đúng 0
Bình luận (0)
Câu 24: Trong mặt phẳng Oxy, cho hai điểm A(1;2) và B(-1;3). Tìm toạ độ điểm M trên trục Oy sao cho tam giác ABM vuông tại B
A. M(0;-2)
B. M(0;4)
C. M(0;5)
D. M(0;-4)
M thuộc Oy \(\Rightarrow M\left(0;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{BM}=\left(1;y-3\right)\end{matrix}\right.\)
ABM vuông tại B \(\Rightarrow\overrightarrow{AB}.\overrightarrow{BM}=0\)
\(\Rightarrow-2+y-3=0\Rightarrow y=5\)
\(\Rightarrow M\left(0;5\right)\)
Đúng 1
Bình luận (0)
CÁC BÁC ƠI ! GIÚP EM VỚI ☘
Trong mặt phẳng Oxy cho 2 điểm A(4;1) và B(0;-2)
a, Tính tọa độ của vectơ \(\overrightarrow{BA}\)
b, Tìm tọa độ điểm C sao cho \(\Delta\)ABC \(\perp\)C
Trong không gian với hệ toạ độ Oxy, cho ba điểm A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là: A.
2
x
+
y
+
2
z
−
5
0.
B.
x
+
2
y
+
5
z
+...
Đọc tiếp
Trong không gian với hệ toạ độ Oxy, cho ba điểm A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:
A. 2 x + y + 2 z − 5 = 0.
B. x + 2 y + 5 z + 5 = 0.
C. x − 2 y + 3 z − 7 = 0.
D. x + 2 y + 5 z − 5 = 0.
Đáp án D
B C → ( − 1 ; − 2 ; − 5 ) ⇒ ( P ) : ( x − 2 ) + 2 ( y + 1 ) + 5 ( z − 1 ) = 0 ⇔ x + 2 y + 5 z − 5 = 0
Đúng 0
Bình luận (0)