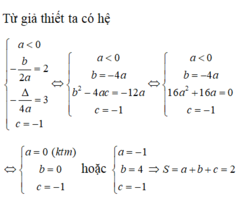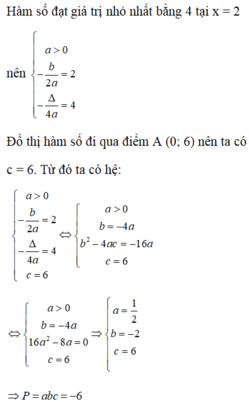Cho hàm số \(y=ax^2+bx+c\) đạt giá trị lớn nhất bằng 5 khi \(x=-2\) và đồ thị đi qua \(A\left(1;-1\right)\). Khi đó giá trị của \(25a-5b+c=...\)

Những câu hỏi liên quan
Biết rằng hàm số y a
x
2
+ bx + c (a
≠
0) đạt giá trị lớn nhất bằng 5 tại x − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S
a
2
+
b
2
+
c
2
A. S −1. B. S 1. C. S 13. D. S 14.
Đọc tiếp
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 5 tại x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = a 2 + b 2 + c 2
A. S = −1.
B. S = 1.
C. S = 13.
D. S = 14.
Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13
Đúng 0
Bình luận (0)
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.
A. S = -1
B. S = 4
C. S = - 4
D. S = 2
xác định hàm số bậc 2 có đồ thị là parabol (p) biết : a, (P) : y= ax^2 + bx + c có giá trị lớn nhất bằng 1 khi x = 2, đồng thời (P) qua M( 4; -3)
Xem chi tiết
Với \(a\ne0\) từ đề bài ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)
\(\Rightarrow a=-1;b=4;c=-3\)
Vậy (P): \(y=-x^2+4x-3\)
Đúng 2
Bình luận (0)
Xác định hàm số y = ax² + bx + c biết hàm đạt GTLN bằng 5 tại x = -2 và đồ thị hàm số đi qua điểm M(1; -1)
y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)
Đúng 0
Bình luận (0)
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.
A. P = -6
B. P = 6
C. P = -3
D. P = 32
Xác định hàm số a b c để hs y=ax^+bx+c =0 có giá trị nhỏ nhất -4/3 khi x= 1/3 và đồ thị hs đi qua điểm A(2;7)
Xem chi tiết
- Từ các giả thiết của đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\-\dfrac{b}{2a}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\2a+3b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\\c=-1\end{matrix}\right.\)
Vậy hàm số trên có dạng : \(3x^2-2x-1=0\)
Đúng 1
Bình luận (0)
cho hàm số y = ax^2 + bx + c(a khác 0). tìm a, b, c biết hàm số đó có gtln = 5 khi x = -2 và đồ thị đi qua M(1;-1)
\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...
Đúng 2
Bình luận (0)
Cho phương trình của (P): y a
x
2
+ bx + c (a
≠
0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng
a
2
+
b
2
+
c
2
A.
a
2
+
b
2
+
c...
Đọc tiếp
Cho phương trình của (P): y = a x 2 + bx + c (a ≠ 0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng a 2 + b 2 + c 2
A. a 2 + b 2 + c 2 = 3
B. a 2 + b 2 + c 2 = 29 16
C. a 2 + b 2 + c 2 = 48 29
D. a 2 + b 2 + c 2 = 5 a 2 + b 2 + c 2 = 209 16
Xác định a,b,c để đồ thị hàm số y=ax^2+bx+c đạt giá trị nhỏ nhất bằng 3/4 khi x=1/2 và đi qua B(1;1)
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}\dfrac{-b}{2a}=\dfrac{1}{2}\\-\dfrac{b^2-4ac}{4a}=\dfrac{3}{4}\\a+b+c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-a\\b^2-4ac=-\dfrac{3}{4}\cdot4a=-3a\\a+b+c=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-a\\\left(-a\right)^2-4ac+3a=0\\a+b+c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=1-a-b=1-a+a=1\\a^2+3a-4a=0\\b=-a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=1\\a=1\\b=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)