Câu 1 Rút gọn biểu thức A - b phần √A - √B + A√B - b√a phần √ab , ( với a > 0; b > 0 )
Câu 2 cho tam giác Abc vuông tại A có đường cao AH biết ab = 12 , bc = 30 . Tính BH và AH
Rút gọn các biểu thức
√a³b +√ab³ - ab phần √ab
Tất cả chung phần √ab
\(\sqrt{a^3b}+\sqrt{ab^3}-\frac{ab}{\sqrt{ab}}\)
<=>\(a\sqrt{ab}+b\sqrt{ab}-\sqrt{ab}\)
<=>\(\left(a+b-1\right)\sqrt{ab}\)
Phần II:Tự luận (7đ)
Câu Phần II:Tự luận (7đ)
Câu 1: a) Tính:
b) Cho biểu thức:
*) Tìm điều kiện xác định và rút gọn biểu thức A.
*) Tìm các giá trị của x để biểu thức A có giá trị âm.
Câu 2: Cho hai hàm số bậc nhất y = (m – 1)x + 2 với m ≠ 1 (d1)
y = (3 – m)x – 2 với m ≠ 3 (d2)
a/ Tìm giá trị của m để đồ thị của hai hàm số đã cho cắt
b/ Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ khi m = 0.
c/ Gọi I là giao điểm của hai đồ thị nói trên. Tìm tọa độ của điểm I (bằng phép toán).
d/ Tính góc hợp bởi đường thẳng (d2) với trục Ox khi m = 0.
Câu 3:Từ điểm M ở ngoài (O; R) vẽ hai tiếp tuyến MA, MB với (O) (A, B là 2
tiếp điểm), vẽ dây AC// OM.
a) Chứng minh OM AB tại H và suy ra OH.OM = R2.
b) MC cắt (O) tại E. Chứng minh 3 điểm B, O, C thẳng hàng và MH.MO = ME.MC.
c) Vẽ AK BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
1: a) Tính: ![]()

b) Cho biểu thức: 
*) Tìm điều kiện xác định và rút gọn biểu thức A.
*) Tìm các giá trị của x để biểu thức A có giá trị âm.
Câu 2: Cho hai hàm số bậc nhất y = (m – 1)x + 2 với m ≠ 1 (d1)
y = (3 – m)x – 2 với m ≠ 3 (d2)
a/ Tìm giá trị của m để đồ thị của hai hàm số đã cho cắt
b/ Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ khi m = 0.
c/ Gọi I là giao điểm của hai đồ thị nói trên. Tìm tọa độ của điểm I (bằng phép toán).
d/ Tính góc hợp bởi đường thẳng (d2) với trục Ox khi m = 0.
Câu 3:Từ điểm M ở ngoài (O; R) vẽ hai tiếp tuyến MA, MB với (O) (A, B là 2
tiếp điểm), vẽ dây AC// OM.
a) Chứng minh OM ![]() AB tại H và suy ra OH.OM = R2.
AB tại H và suy ra OH.OM = R2.
b) MC cắt (O) tại E. Chứng minh 3 điểm B, O, C thẳng hàng và MH.MO = ME.MC.
c) Vẽ AK![]() BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
mọi người giúp mik với
Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
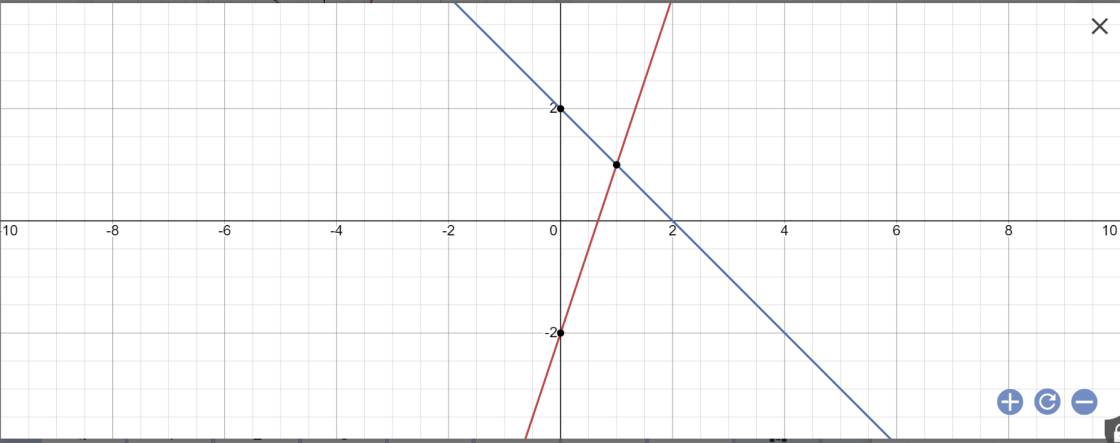
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)
15. Tìm các số nguyên dương n nhỏ hơn 14 sao cho phân số n phần 14 có thể rút gọn được. Rút gọn phân số đó ứng với mỗi giá trị tìm được của n.
16. Viết các phân số tối giản a phần b (a>0, b>0), biết rằng ab = 36.
17.Tìm các phân số a phần b (a>0, b>0) có giá trị bằng: a) 21 phần 28, biết ƯCLN(a,b)=15 b) 21 phần 35, biết ƯCLN(a,b)=30. c) 36 phần 45, biết BCNN(a,b)=300. d) 15 phần 35, biết ƯCLN(a,b).BCNN(a,b)= 3549.
nhìn rối quá ạ :v tách ra từng bài một hộ tớ
Bài 16:
1/36; 36/1; 4/9; 9/4
Bài 17:
a: a/b=3/4=45/60
b: a/b=3/5=90/150
Cho biểu thức \(M=\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}-\dfrac{a}{\sqrt{a}+\sqrt{b}}-\dfrac{b}{\sqrt{b}-\sqrt{a}}\) với a,b>0 và \(a\ne b\) . Rút gọn M và tính giá trị biểu thức M biết \(\left(1-a\right).\left(1-b\right)+2\sqrt{ab}=1\)
\(M=\dfrac{a\sqrt{a}-b\sqrt{b}-a\sqrt{a}+a\sqrt{b}+b\sqrt{a}+b\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\\ M=\dfrac{a\sqrt{b}+b\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\\ M=\dfrac{\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)
\(\left(1-a\right)\left(1-b\right)+2\sqrt{ab}=1\\ \Leftrightarrow1-a-b+ab+2\sqrt{ab}=1\\ \Leftrightarrow a+b-ab-2\sqrt{ab}=0\\ \Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2=ab\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{a}-\sqrt{b}=\sqrt{ab}\\\sqrt{a}-\sqrt{b}=-\sqrt{ab}\end{matrix}\right.\)
Với \(\sqrt{a}-\sqrt{b}=\sqrt{ab}\Leftrightarrow M=\dfrac{\sqrt{ab}}{\sqrt{ab}}=1\)
Với \(\sqrt{a}-\sqrt{b}=-\sqrt{ab}\Leftrightarrow M=\dfrac{\sqrt{ab}}{-\sqrt{ab}}=-1\)
\(M=\dfrac{a\sqrt{a}-b\sqrt{b}-a\left(\sqrt{a}-\sqrt{b}\right)+b\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{a\sqrt{b}+b\sqrt{a}}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)
\(\left(1-a\right)\left(1-b\right)+2\sqrt{ab}=1\)
\(\Leftrightarrow a+b-ab-2\sqrt{ab}=0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2=ab\Leftrightarrow\sqrt{a}-\sqrt{b}=\sqrt{ab}\)
\(M=\dfrac{\sqrt{ab}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}}{\sqrt{ab}}=1\)
Cho biểu thức
A=(x phần x2-4 + 2 phần 2-x + 1 phần 2+x).x+2 phần 2
a) Tìm điều kiện của x để biểu thức A xác định
b) Rút gọn A
c) Tính giá trị của A khi x=-1
`A=(x/[x^2-4]+2/[2-x]+1/[2+x]).[x+2]/2`
`a)ĐK: x \ne +-2`
`b)` Với `x \ne +-2` có:
`A=[x-2(x+2)+x-2]/[(x-2)(x+2)].[x+2]/2`
`A=[x-2x-4+x-2]/[x-2]. 1/2`
`A=[-3]/[x-2]`
`c)x=-1` t/m đk `=>` Thay `x=-1` vào `A` có: `A=[-3]/[-1-2]=1`
Kết quả rút gọn của biểu thức a + a b b + a b (với a, b > 0) là ?
A. a b
B. a b
C. a b
D. a b
Cho biểu thức
A=a+b-√ab/a√a+b√b - √a-√b-1/a-b
( với a>0,b>0,a khác b)
a) Rút gọn b+a
b) Tính giá trị của A biết a-b=1
a: \(A=\dfrac{1}{\sqrt{a}+\sqrt{b}}-\dfrac{\sqrt{a}-\sqrt{b}-1}{a-b}\)
\(=\dfrac{\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}+1}{a-b}=\dfrac{1}{a-b}\)
b: Khi a-b=1 thì A=1/1=1
Câu 2 (1,0 điểm). Tìm x biết.
a) b)
Câu 3 (1,0 điểm). Cho biểu thức ; với
a) Rút gọn biểu thức P .
b) Tìm điều kiện của x để P > 0
Câu 2:
\(a,ĐK:x\ge-3\\ PT\Leftrightarrow6\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+3}=2\\ \Leftrightarrow2\sqrt{x+2}=2\\ \Leftrightarrow\sqrt{x+2}=1\\ \Leftrightarrow x+2=1\\ \Leftrightarrow x=-1\left(tm\right)\\ b,\Leftrightarrow\sqrt{\left(2x-3\right)^2}=2017\Leftrightarrow\left|2x-3\right|=2017\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=2017\\3-2x=2017\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1010\\x=-1007\end{matrix}\right.\)
Câu 3:
\(a,P=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}+3}\\ b,P=\dfrac{-3}{\sqrt{x}+3}< 0,\forall x\left(-3< 0;\sqrt{x}+3>0\right)\\ \Leftrightarrow x\in\varnothing\)