Cho A và B là hai biến cố độc lập với P(A) = 0,6; P(B) = 0,3. Tính
a) P(A ∪ B);
b) P ( A ∪ B )
Cho hai biến cố \(A\) và \(B\) độc lập với nhau. Biết \(P\left( A \right) = 0,9\) và \(P\left( B \right) = 0,6\). Hãy tính xác suất của biến cố \(A \cup B\).
Vì A và B là hai biến cố độc lập, nên `P(A∩B) = P(A) * P(B)`
Ta có:
`P(A∪B) = P(A) + P(B) - P(A) * P(B)`
`= 0,9 + 0,6 - 0,9 * 0,6`
`= 0,9 + 0,6 - 0,54`
`= 0,96`
Vậy xác suất của biến cố `A∪B` là 0,96.
$HaNa$
Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.
Hai biến cố A và B xung khắc khi và chỉ khi \(A \cap B = \emptyset \Rightarrow P\left( {AB} \right) = 0\)
Vì P(A) > 0, P(B) > 0 nên \(P\left( A \right).P\left( B \right) > 0\)
\( \Rightarrow P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\)
Vậy hai biến cố A và B không độc lập.
Cho A và B là hai biến cố độc lập với \(P\left(A\right)=0,6;P\left(B\right)=0,3\). Tính
a) \(P\left(A\cup B\right)\)
b) \(P\left(\overline{A}\cup\overline{B}\right)\)
a) \(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right)=P\left(A\right)+P\left(B\right)-P\left(A\right)P\left(B\right)\)
\(=0,6+0,3-0,18=0,72\)
b) \(P\left(\overline{A}\cup\overline{B}\right)=1-P\left(AB\right)=1-0,18=0,82\)
Cho \(A\) và \(B\) là hai biến cố thoả mãn \(P\left( A \right) = 0,5;P\left( B \right) = 0,7\) và \(P\left( {A \cup B} \right) = 0,8\).
a) Tính xác suất của các biến cố \(AB,\bar AB\) và \(\bar A\bar B\).
b) Hai biến cố \(A\) và \(B\) có độc lập hay không?
tham khảo
a)\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right).\)
Suy ra \(P\left(AB\right)=0,4\)
\(P\left(\overline{A}B\right)=P\left(B\right)-P\left(AB\right)=0,7-0,4=0,3\)
\(P\left(\overline{A}\overline{B}\right)=1-P\left(A\cup B\right)=0,2\)
b) Vì \(P\left(AB\right)\ne P\left(A\right).P\left(B\right)\) nên A và B không độc lập.
Cho P ( A ) = 1 4 ; P ( A ∪ B ) = 1 2 .Biết A và B là hai biến cố độc lập thì P(B) bằng
![]()
![]()
![]()
![]()
Cho \(A\) và \(B\) là hai biến cố độc lập. Biết \(P\left( A \right) = 0,4\) và \(P\left( B \right) = 0,5\). Xác suất của biến cố \(A \cup B\) là
A. 0,9.
B. 0,7.
C. 0,5.
D. 0,2.
tham khảo
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right)=0,7\)
\(\Rightarrow D\)
Cho P A = 1 4 ; P A ∪ B = 1 2 . Biết A và B là hai biến cố độc lập thì P(B) bằng
A. 2 3
B. 1 2
C 1 4
D. 1 3
Đáp án D
Ta có ![]()
Vì A và B là hai biến cố độc lập, do đó
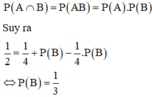
Cho P A = 1 4 ; P A ∪ B = 1 2 . Biết A và B là hai biến cố độc lập thì P B bằng
A. 1 4
B. 1 3
C. 1 2
D. 2 3
Cho hai biến cố \(A\) và \(B\) độc lập với nhau.
a) Biết \(P\left( A \right) = 0,3\) và \(P\left( {AB} \right) = 0,2\). Tính xác suất của biến cố \(A \cup B\).
b) Biết \(P\left( B \right) = 0,5\) và \(P\left( {A \cup B} \right) = 0,7\). Tính xác suất của biến cố \(A\).
a) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) \Rightarrow P\left( B \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{2}{3}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{23}}{{30}}\)
b) \(A\) và \(B\) là hai biến cố độc lập \( \Rightarrow P\left( {AB} \right) = P\left( A \right)P\left( B \right) = 0,5.P\left( A \right)\)
\(\begin{array}{l}P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) \Leftrightarrow 0,7 = P\left( A \right) + 0,5 - 0,5.P\left( A \right)\\ \Leftrightarrow 0,5P\left( A \right) = 0,2 \Leftrightarrow P\left( A \right) = 0,4\end{array}\)