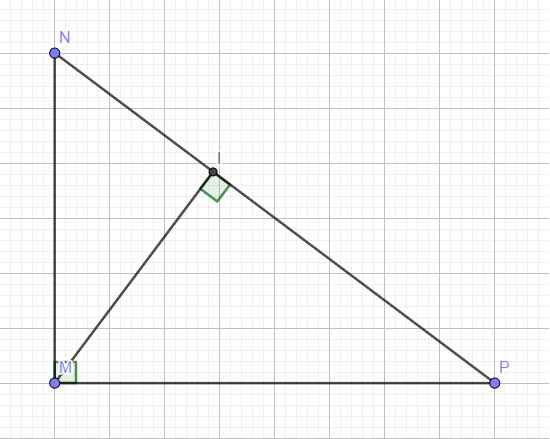
Cho ∆ MNP vuông tại M, đường cao MI. Biết 𝑁̂= 60độ ; NP=5cm.Tính MN và MP .(Sử dụng bảng tỉ số lượng giác của các góc đặc biệt để tính TSLG của góc 60độ)

Những câu hỏi liên quan
Cho tam giác MNP vuông tại M, đường cao MI . Biết MI = 16 , IN = 25 . Tính các đoạn thẳng IP, MN, MP , PN
Xét `\triangle MNP` vuông tại `M` có `MI` là đường cao
`@MN=\sqrt{MI^2+NI^2}=\sqrt{881}`.
`@NP=[MN^2]/[NI]=35,24`.
`@MP=\sqrt{NP^2-MN^2}=[16\sqrt{881}]/25`.
`@IP=\sqrt{MP^2-MI^2}=10,24`.
Đúng 0
Bình luận (0)
Cho tg MNP vuông tại M. Đường cao MI, biết MN/MP=3/4, MI=48/5 cm. Tính:
a, Độ dài các đoạn thẳng MN, MP, NP
b, Diện tích tg MIP
Cho tam giác MNP vuông tại M, đường cao MI. Biết \(\dfrac{MN}{MP}=\dfrac{3}{4}\); MI=\(\dfrac{48}{5}\) cm.Tính:
a) Độ dài các đoạn thẳng MN, MP, NP.
b) Diện tích tam giác MIP.
\(\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow MN=\dfrac{3}{4}MP\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{MI^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{48}{5}\right)^2}=\dfrac{1}{\left(\dfrac{3}{4}MP\right)^2}+\dfrac{1}{MP^2}\)
\(\Rightarrow MP^2=\dfrac{20736}{625}\Rightarrow MP=\dfrac{144}{25}\)
\(\Rightarrow MN=\dfrac{3}{4}MP=\dfrac{108}{25}\)
\(NP=\sqrt{MN^2+MP^2}=\dfrac{36}{5}\)
b. Áp dụng hệ thức lượng:
\(MP^2=IP.NP\Rightarrow IP=\dfrac{MP^2}{NP}=\dfrac{576}{125}\)
\(S_{MIP}=\dfrac{1}{2}IP.MI=\dfrac{13824}{625}\)
Đúng 2
Bình luận (0)
Cho tam giác MNP vuông tại M, đường cao MI(I thuộc NP). Cho PI=6cm, MP= 10 cm. a) Tính PN, MI, góc MNP b) Tính chu vì tam giác MNP c) Gọi H,K lần lượt là hình chiếu của I trên MN, MP. Tính IK
a: ΔPIM vuông tại I
=>IP^2+IM^2=MP^2
=>IM^2=10^2-6^2=64
=>IM=8(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên PI*PN=PM^2
=>PN=10^2/6=50/3(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên MI^2=IN*IP
=>IN=8^2/6=32/3(cm)
Xét ΔMNP vuông tại M có sin MNP=MP/PN
=10:50/3=3/5
=>góc MNP=37 độ
b: C=MN+NP+MP
=10+40/3+50/3
=10+90/3
=10+30
=40(cm)
c: Xét ΔIMP vuông tại I có IK là đường cao
nên IK*PM=IP*IM
=>IK*10=6*8=48
=>IK=4,8(cm)
Đúng 1
Bình luận (0)
Bài 1: Cho ∆MNP vuông tại M; đường cao MI. Biết và MI = 9,8cm a/ Tính MN; MP; NP b/ Tính diện tích tam giác MIP Bài 2: Cho ∆CDE có 3 góc nhọn, đường cao CH. Gọi M, N theo thứ tự là hình chiếu của H trên CD; CE. a/ Chứng minh : CD. CM = CE. CN b/ Chứng minh ∆CMN đồng dạng với ∆CED.
1.cho đoạn thẳng AB=20cm, CD=4dm thì?
2.tam giác MNP vuông tại M và đường cao MH có bao cặp tam giác đồng dạng?
3.tam giác DEF đồng dang với MNP (theo tỉ số k) có DH và MI lần lượt là đường cao của tam giác DEF và tam giác MNP thì tỉ số đường cao là?
1: AB=20cm
=>AB=2dm
=>\(\dfrac{AB}{CD}=\dfrac{2}{4}=\dfrac{1}{2}\)
2: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔHNM đồng dạng với ΔMNP
Xét ΔHPM vuông tại H và ΔMPN vuông tại M có
\(\widehat{P}\) chung
Do đó: ΔHPM đồng dạng với ΔMPN
Xét ΔHMN vuông tại H và ΔHPM vuông tại H có
\(\widehat{HMN}=\widehat{P}\left(=90^0-\widehat{N}\right)\)
Do đó: ΔHMN~ΔHPM
Câu 3:
ΔDEF~ΔMNP
=>\(\widehat{E}=\widehat{N}\) và \(\dfrac{DE}{MN}=k\)
Xét ΔDHE vuông tại H và ΔMIN vuông tại I có
\(\widehat{E}=\widehat{N}\)
Do đó: ΔDHE đồng dạng với ΔMIN
=>\(\dfrac{DH}{MI}=\dfrac{DE}{MN}=k\)
Đúng 0
Bình luận (0)
Cho t.giác MNP vuông tại M, có đg cao MI. Tính MI, biết rằng :
a) MN=6cm; MP=8cm
b) MN=9cm; MP=16cm
c) MN=\(\sqrt{2}\)cm; \(\sqrt{3}\)cm
Giúp mình với ạ !!! ![]()
a, Áp dụng định lý Pytago vào tam giác MNP
\(MN^2+MP^2=NP^2\\ \Rightarrow NP=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có \(MN\times MP=MI\times NP\\ \Rightarrow MI=\dfrac{6\times8}{10}=4,8\left(cm\right)\)
b, Áp dụng định lý Pytago vào tam giác MNP
\(MN^2+MP^2=NP^2\\ \Rightarrow NP=\sqrt{9^2+16^2}=\sqrt{337}\left(cm\right)\)
Ta cs
\(MN\times MP=MI\times NP\\ \Rightarrow MI=\dfrac{9\times16}{\sqrt{337}}\approx7,8\left(cm\right)\)
c, \(MN^2+MP^2=NP^2\\ \Rightarrow NP=\sqrt{\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2}=\sqrt{5}\left(cm\right)\)
Ta có \(MN\times MP=MI\times NP\\ \Rightarrow MI=\dfrac{\sqrt{2}\times\sqrt{3}}{\sqrt{5}}=\dfrac{\sqrt{30}}{5}\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác MNP cân tại M Vẽ mi vuông góc với NP tại I
Chứng minh MI là đường trung trực của N P
vẽ IE vuông góc với MN tại A, IB vuông góc với MP tại B chứng minh tam giác IAB cân
Giả sử góc MNP = 45° MN = 2 cm Tính NP
Giả sử góc MNP = 30 độ Chứng minh tam giác AIB đều
cho ∆MNP vuông tại M. đường cao MK vẽ đường tròn tâm M bán kính MK.gọi KD là đường kính của đường của đường tròn (M,MK) tiếp tuyến của đường tròn tại D cắt MP ở I.
a, CMR ∆NIP cân.
b, gọi H là hình chiếu của M trên MI. tính độ dài MH biết KP=5cm,góc P=35°.
c, chứng minh MI là tiếp tuyến của đường tròn (M;MK)