D là đáp án đúng (do I là giao điểm AC và BM \(\Rightarrow I=\left(SAC\right)\cap\left(SBM\right)\)

\(\Rightarrow SI=\left(SAC\right)\cap\left(SBM\right)\)

D

Xét ΔDEM và ΔBEA có 

\(\widehat{DEM}=\widehat{BEA}\)(hai góc đối đỉnh)

\(\widehat{DME}=\widehat{BAE}\)(hai góc so le trong, DM//AB)

Do đó: ΔDEM\(\sim\)ΔBEA(g-g)

Suy ra: \(\dfrac{EM}{EA}=\dfrac{DM}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(1)

Xét ΔMFC và ΔBFA có 

\(\widehat{MFC}=\widehat{BFA}\)(hai góc đối đỉnh)

\(\widehat{MCF}=\widehat{BAF}\)(hai góc so le trong, AB//MC)

Do đó: ΔMFC\(\sim\)ΔBFA(g-g)

Suy ra: \(\dfrac{FM}{FB}=\dfrac{CM}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)(2)

Ta có: M là trung điểm của CD(gt)

nên CM=DM(3)

Từ (1), (2) và (3) suy ra \(\dfrac{EM}{EA}=\dfrac{FM}{FB}\)

Xét ΔMAB có 

E\(\in\)AM(gt)

\(F\in BM\)(gt)

\(\dfrac{EM}{EA}=\dfrac{FM}{FB}\)(cmt)

Do đó: EF//AB(Định lí Ta lét đảo)

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)

⇔ AB = DM và AB // DM

Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.

b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC

c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2

Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)

d) Ta có :

Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)

⇒ BC = AM = 3 (cm)

Ta có:

M là trung điểm của DC nên

SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)

Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)

⇔ SABD = SBMD = 3 (cm2)

Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)

Mày N Mày Chết M Mày Đi Kêu Cặk

2: Xét ΔEAB và ΔEMD có

góc EAB=góc EMD

góc EBA=góc EDM

=>ΔEAB đồng dạng với ΔEMD

=>EA/EM=AB/MD=AB/MC

=>ME/EA=MC/AB

Xét ΔFMC và ΔFBA có

góc FMC=góc FBA

góc MFC=góc BFA

=>ΔFMC đồng dạng với ΔFBA

=>FM/FB=MC/BA=ME/MA

=>EF//AB

=>FE/AB=MF/MB=1:(1+BF/MF)=1:(1+AB/CD)=1:(AB+CD)/CD

=CD/(AB+CD)

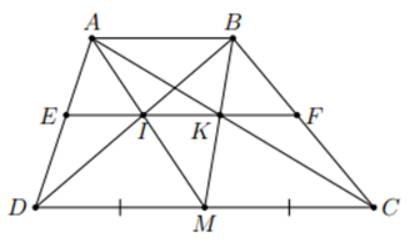
a) Vì AB // CD áp dụng định lý Ta-lét ta có:

\(\dfrac{IM}{IA}\)=\(\dfrac{MD}{AB}\) 

                   \(\Rightarrow\)  \(\dfrac{IM}{IA}\)=\(\dfrac{KM}{KB}\) (Vì MC = MD) 

\(\dfrac{KM}{KB}\)=\(\dfrac{MC}{AB}\)

  Do đó theo định lý Ta-lét đảo ta có IK // AB 

Vì IK // AB // CD nên theo định lý Ta-lét :

\(\dfrac{IE}{DM}\)=\(\dfrac{AI}{AM}\)=\(\dfrac{BI}{BD}\)=\(\dfrac{IK}{DM}\)=> EI = IK 

Tương tự ta có FK =IK nên ta có EI = IK = KF

 1] 
a] 

Ta có: 
AI/IM = AB/DM 
BK/KM = AB/MC 

Do DM =MC 
=> AI/IM = BK/KM 

=> IK//AB 

b] 
IE/DM = AI/AM 
KF/MC = BK/BM 

Mà AI/AM = BK/BM (do IK//AB) 

=> IE/DM = KF/MC mà DM=MC 
=> IE = KF 

2] 
a} 
Ta có: 
AE/EK = AB/DK 
BF/FI = AB/CI 
Do ABID và ABCK là h..b.hành 
=> CK=DI =AB 
=> DK = CI = CD -AB 
=> AE/EK = NF/FI 

=> EF//AB 

b} 

Ta có EF/CK =AF/AC = AB/CD 
=> EF.CD = CK.AB = AB^2 (do CK =AB) 

3] 
a} 
Ta có: 
MB/MF = MC/MA (Xét BC//AF) 
ME/MB = MC/MA (Xét CE//AB) 

=> MB/MF = ME/MB 
=> MB^2 = ME.MF 

b} 

BM/MF = MC/AC (Xét BC//AF) 
BM/ME = AM/AC (Xét CE//AB) 

=> BM/MF + BM/ME = MC/AC + AM/AC =1 

=> BM/MF + BM/ME =1 

=> 1/BF+1/BE=1/BM

a. -Xét △ABH có: AB//DM (gt)

\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{DM}\) (định lí Ta-let)

Mà \(DM=\dfrac{1}{2}CD\) (M là trung điểm CD).

\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)

b. Sửa đề: C/m HK//AB.

-Xét △ABK có: AB//CM (gt)

\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{CM}\) (định lí Ta-let)

Mà \(CM=\dfrac{1}{2}CD\) (M là trung điểm CD).

\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)

-Xét △ABM có: \(\dfrac{AH}{HM}=\dfrac{AK}{KC}\left(=\dfrac{2AB}{CD}\right)\)

\(\Rightarrow\)HK//AB.

c. -Xét △ABM có: HK//AB (cmt).

\(\Rightarrow\dfrac{AB}{HK}=\dfrac{AM}{HM}\) (định lí Ta-let).

\(\Rightarrow\dfrac{AB-HK}{HK}=\dfrac{AM-HM}{HM}\)

\(\Rightarrow\dfrac{AB}{HK}-1=\dfrac{AH}{HM}\)

Mà \(\dfrac{AH}{HM}=\dfrac{2AB}{CD}\left(cmt\right)\)

\(\Rightarrow\dfrac{AB}{HK}=\dfrac{2AB}{CD}\)

\(\Rightarrow\dfrac{a}{HK}=\dfrac{2a}{b}\)

\(\Rightarrow HK=\dfrac{b}{a}\)