Cho tam giác ABC vuông tại A, đường cao AH, kẻ HE vuông góc AB, Hf vuông góc AC ( E thuộc AB; F thuộc AC)
Chứng minh \(\sqrt{S_{BEH}}+\sqrt{S_{CFH}}=\sqrt{S_{ABC}}\)
Helppp mik cần gấp ạ

Những câu hỏi liên quan
Cho tam giác ABC vuông tại a có đường cao AH 1.cho biết AB =3cm , AC=4cm , tính độ dài các đoạn BC,HB,HC,AH 2. Kẻ HE vuông góc với AB , HF vuông góc với AC ( E thuộc AB , F thuộc AC )
a: BC=5cm
AH=2,4cm
BH=1,8cm
CH=3,2cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC. Kẻ HE vuông góc AB (E thuộc AB, HF vuông góc AC (F thuộc AC
a, Tứ giác AEHF là hình gì? Vì sao?
b, Chứng minh BE.CH=AE.BH
Cho tam giác ABC vuông tại A, đường cao AH, kẻ HE vuông góc với AB (E thuộc AB), kẻ HF vuông góc với AC (F thuộc AC)
a, Chứng minh AE . AB = AF. AC = BH . HC
b, Cho AB =\(\sqrt{12}\) cm, HC = 4cm. Tính AB, BC
c, AE . EB + AF . FC = BH . HC
d, AH\(^3\) = BC. HE. HF
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, Kẻ HF vuông góc với AC tại F. Chứng minh tứ giác BEFC nội tiếp
Gợi ý: A F E ^ = A H E ^ (tính chất hình chữ nhật và A H E ^ = A B H ^ (cùng phụ B H E ^ )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, Kẻ HF vuông góc với AC tại F. Chứng minh tứ giác BEFC nội tiếp.
Ta có: \(\widehat{C_1}=\widehat{A_1}\)(cùng phụ với \(\widehat{B_1}\)) \(\left(1\right)\)
Xét tứ giác AEHF có: \(\widehat{A}=\widehat{E}=\widehat{F}=\widehat{H}=90^o\)
=> tứ giác AEHF là h.c.n
=> \(\widehat{A_1}=\widehat{E_1}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{E_1}=\widehat{C_1}\)
vì \(\widehat{E_1}+\widehat{BEF}=180^o\)
\(\Rightarrow\widehat{C_1}+\widehat{BEF}=180^o\) mà 2 góc đối nhau
=> tứ giác BEFC nội tiếp
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm. AC=8cm
a) Tính BC,AH, góc B,góc C
b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC
c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
Cho tam giác ABC vuông tại A (AB AC), có AH là đường cao . Kẻ HE
vuông góc AB tại E, kẻ HF vuông góc AC tại Ƒ
A) Chứng minh tứ giác AEHF là hình chữ nhật
b) lấy điểm M kẻ đường thẳng song song AH , đường thẳng này cắt tia HF tại N . Chứng minh
tứ giấc EFMH là hình bình hành
c) một mảnh đất hình chữ nhật có chiều dài là (2x+3)² mét vuông và chiều rộng là
(2x-1)² . Biết chiều dài hơn chiều rộng là 36 mét . Tính chu vi mảnh đất
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), có AH là đường cao . Kẻ HE
vuông góc AB tại E, kẻ HF vuông góc AC tại Ƒ
A) Chứng minh tứ giác AEHF là hình chữ nhật
b) lấy điểm M kẻ đường thẳng song song AH , đường thẳng này cắt tia HF tại N . Chứng minh
tứ giấc EFMH là hình bình hành
c) một mảnh đất hình chữ nhật có chiều dài là (2x+3)² mét vuông và chiều rộng là
(2x-1)² . Biết chiều dài hơn chiều rộng là 36 mét . Tính chu vi mảnh đất
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F thuộc AB) và kẻ HE vuông góc vói AC (E thuộc AC)a, Chứng minh:
A
F
E
^
A
C
B
^
b, Đường thẳng EF cắt BC tại M. Chứng minh ME.MF MB.MC
Đọc tiếp
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F thuộc AB) và kẻ HE vuông góc vói AC (E thuộc AC)
a, Chứng minh: A F E ^ = A C B ^
b, Đường thẳng EF cắt BC tại M. Chứng minh ME.MF = MB.MC
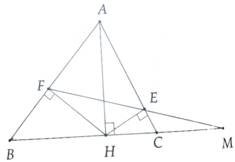
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a,bc=5cm,°C=30°
a)giải tam giác vuông ABC.
b)tính đường cao AH
c)kẻ HE vuông góc AB TẠI E VÀ HF VUÔNG GÓC AC TẠI F CM :AH\3=BE.CF.BC cần gấp 

Câu 15:
a: ĐKXĐ: x>=0; x<>1
Đúng 0
Bình luận (0)














