Cho ΔABC có AB=AC (góc A nhọn). Kẻ BH vuông góc với (H∈AC), kẻ CK vuông góc với AB(K∈AB); BH cắt CK tại I
A) CM: BH=CK
b)CM: ΔIBK=ΔICH. So sánh IK và IC
c) Gọi M là trung điểm của BC. CM: A,I,M thẳng hàng
Cho tam giác nhọn ABC. Kẻ Bh vuông góc với AC (H thuộc AC) kẻ CK vuông góc với AB (K thuộc AB). So sánh góc ABH vói góc ACK
Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC ( H thuộc AC), kẻ CK vuông góc với AB ( K thuộc AB). Hãy so sánh ∠(ABH) và ∠(ACK.)
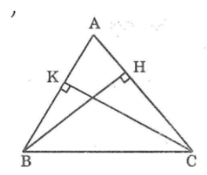
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)
Bài 8 :
Cho ΔABC cân tại A có M là trung điểm của BC
a) Vẽ hình
b) Chứng minh rằng : AM là đường trung trực của ΔABC
c) Kẻ BH vuông góc với AC (H thuộc AC), CK vuông góc với AB (K thuộc AB). Chứng minh rằng : BH = CK
d) Chứng minh rằng : HK//BC
e) Gọi O là giao điểm của BH và CK
Chứng minh rằng : ba điểm AOM thẳng hàng
Cho Δ ABC có ba góc nhọn. Kẻ BH vuông với AC ( H \(\in\) AC ) và kẻ CK vuông với AB (K \(\in\) AB).
a) Tìm các góc phụ với góc A có trong hình vẽ;
Hãy so sánh góc ABH và góc ACK; góc BIK và góc CIH ( với I là giao điểm của BH và CK).
a: \(\widehat{ABH};\widehat{ACK}\) là các góc phụ với A
b: Vì \(\widehat{ABH}+\widehat{A}=90^0\)
mà \(\widehat{ACK}+\widehat{A}=90^0\)
nên \(\widehat{ABH}=\widehat{ACK}\)
\(\widehat{BIK}=\widehat{CIH}\)(hai góc đối đỉnh)
Cho tam giác ABC cân ở A. Kẻ BH vuông góc với AC(H thuộc AC). Kẻ CK vuông góc với AB(K thuộc AB). chứng minh AH=AK
Ta có: ΔABC cân tại A
=> Góc B = góc C
=> AB = AC
Xét 2 ΔKBC và ΔHCB có
Góc B = góc C
BC chung
Góc BKC = góc BHC = 90o
=> ΔKBC = ΔHCB (c - g - c)
=> BK = HC
Mà AB = AC (cmt)
=> AK = AH (dpcm)
Xét tam giác vuông \(ABH\)và tam giác \(ACK\) có :
\(AB=AC\) ( tam giác ABC cân tại A )
A chung
Vậy \(\Delta ABH=\Delta ACK\)
\(\Leftrightarrow AH=AK\)
Cho tam giác ABC nhọn. Qua B kẻ BH vuông góc AC ( H thuộc AC ); qua C kẻ CK vuông góc AB ( K thuộc AB ). Trên tia đối của tia BH lấy điểm M sao cho BM = AC, trên tia đối của tia CK lấy điểm N sao cho CN = AB. Chứng minh:
a) Góc ABH = góc ACK
b) Tam giác ABM = tam giác NCA
c) AM vuông góc với AN
Cho tam giác ABC nhọn. Qua B kẻ BH vuông góc AC ( H thuộc AC ); qua C kẻ CK vuông góc AB ( K thuộc AB ). Trên tia đối của tia BH lấy điểm M sao cho BM = AC, trên tia đối của tia CK lấy điểm N sao cho CN = AB. Chứng minh:
a) Góc ABH = góc ACK
b) Tam giác ABM = tam giác NCA
c) AM vuông góc với AN
Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC (H∈AC), kẻ CK vuông góc với AB (K ∈ AB)
a, CM: AH = AK
b, Gọi I là giao điểm của BH và CK. CM AI là trung trực của HK
c, Kẻ Bx vuông góc với AB tại B, gọi E là giao điểm của Bx với AC, CM BC là phân giác của góc HBE
d, So sánh CH với CE
kẻ hình với làm giúp mình với ạ
a: Xét ΔAHB vuông ạti H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>IH=IK
=>AI là trung trực của KI
c: góc EBC+góc ABC=90 độ
góc HBC+góc ACB=90 độ
góc ABC=góc ACB
=>góc EBC=góc HBC
=>BC là phân giác của góc HBE
2, Cho tam giác ABC, kẻ BH vuông góc với AC ( A thuộc AC ); CK vuông góc với AB ( K thuộc AB ). Bt BH vuông góc với CK . Chứng minh tam giác ABC cân