cho ΔABC cân tại A. BD⊥AC, EC⊥AB; BD cắt CE ở I. Chứng minh:
a, BE=CD
b, AI là tia phân giác của góc BAC
c, Biết góc BAC=76độ. Tính góc ACB, góc BIC, góc ACB

Những câu hỏi liên quan
Cho ΔABC vuông tại A, BD là tia p/g của góc ABD(D∈AC). DE⊥BC tại E. AB cắt DE tại K.
a, ΔBAE cân
b, Biết AD=6CM. AC=16cm. EC=?
C, AE//CK
a.Xét ΔABD và ΔIBD có:
BAD=BID=90 độ
BD chung
ABD=IBD (do BD là phân giác góc ABC)
=>ΔABD=ΔIBD (ch-gn)
b.Ta có: ΔABD=ΔIBD (cm câu a)
=>AB=IB (2 cạnh tương ứng)
=>ΔABI cân tại B
Lại có: BD là đường phân giác góc B
=>BD đồng thời là đường cao
=>BD⊥AI
c.Ta có: ΔABD=ΔIBD (cm câu a)
=>AD=ID (2 cạnh tương ứng)
Xét ΔDAK và ΔDIC có:
DAK=DIC (=90 độ)
DA=DI (cmt)
ADK=IDC (2 góc đối đỉnh)
=>ΔDAK=ΔDIC (g.c.g)
=>DK=DC (2 cạnh tương ứng)
d.Vì ΔABC vuông tại A nên:
=>BC²=AB²+AC²
<=>BC²=6²+8²
<=>BC²=100
<=>BC=√100=10 (cm)
Ta có: BI+IC=BC
=>IC=BC-BI
Lại có: AB=BI (cm câu b)
=>IC=BC-AB
=>IC=10-6=4 (cm)
Vậy IC=4 cm.
Đúng 1
Bình luận (1)
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
Suy ra: BA=BE(hai cạnh tương ứng)
Xét ΔBAE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
a) Xét ∆ABD và ∆EBD:
BD cạnh chung
\(\widehat{BAD}=\widehat{BED}=90^o\)
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> ∆ABD=∆EBD (ch.gn)
=> AB=BE (2 cạnh t/ứ)
=> ∆ABE cân tại A
b) Ta có: DC=AC-AD=16-6=10 (cm)
Theo câu a: ∆ABD=∆EBD
=> AD=ED=6
Áp dụng định lý Py-ta-go vào tam giác EDC vuông tại E, ta có:
\(DC^2=EC^2+DE^2\)
\(\Leftrightarrow10^2=6^2+EC^2\Rightarrow EC^2=10^2-6^2=64=8^2\)
\(\Rightarrow EC=8\left(cm\right)\)
c) Xét ∆ADK và ∆EDC:
AD=ED(cm ở b)
\(\widehat{ADK}=\widehat{EDC}\) (2 góc đối đỉnh)
\(\widehat{DAK}=\widehat{DEC}=90^o\)
=> ∆ADK=∆EDC (g.c.g)
=> AK=EC (2 cạnh t/ứ)
Mà AB=BE (cm ở a)
=> AK+AB=EC+BE
<=> BK=BC
=> ∆BCK cân ở B
Theo câu a: ∆ABE cân ở B
=> \(\widehat{BAE}=\dfrac{180^o-\widehat{B}}{2}\)
Lại có ∆BKC cân ở B(cmt)
=> \(\widehat{BKC}=\dfrac{180^o-\widehat{B}}{2}\)
=> \(\widehat{BAE}=\widehat{BKC}\)
Mà 2 góc này ở vị trí đồng vị
=> AE//KC
Đúng 1
Bình luận (0)
Cho ΔABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên AC sao cho BD = CE.
a) CMR: ΔABE = ΔACD
b) Gọi I là giao điểm của BE và CD. CMR: ΔBID = ΔCIE
c) CMR: AI là tia phân giác của góc A và AI ⊥ BC
d) Tìm vị trí của D, E để BD = DE = EC
cho ΔABC cân tại A (A<90\(^o\)). Kẻ BD⊥AC(D∈AC), CE⊥AB(E∈AB). BD và CE cắt nhau tại H.
a, ΔABD = ΔACE
b, so sánh góc ABD và góc ACE
c, Kéo dài AH cắt BC tại K. C/M AK⊥BC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>góc ABD=góc ACE
c: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>AH vuông góc BC tại K
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A ( góc A < 90 độ ) . Kẻ BD ⊥ AC tại D , kẻ CE ⊥ AB tại E
a, Chứng minh ΔADE CÂN
b, DE // BC
c, Gọi I là giao diểm của BD và CE . Chứng minh IB = IC
d, AI ⊥ BC
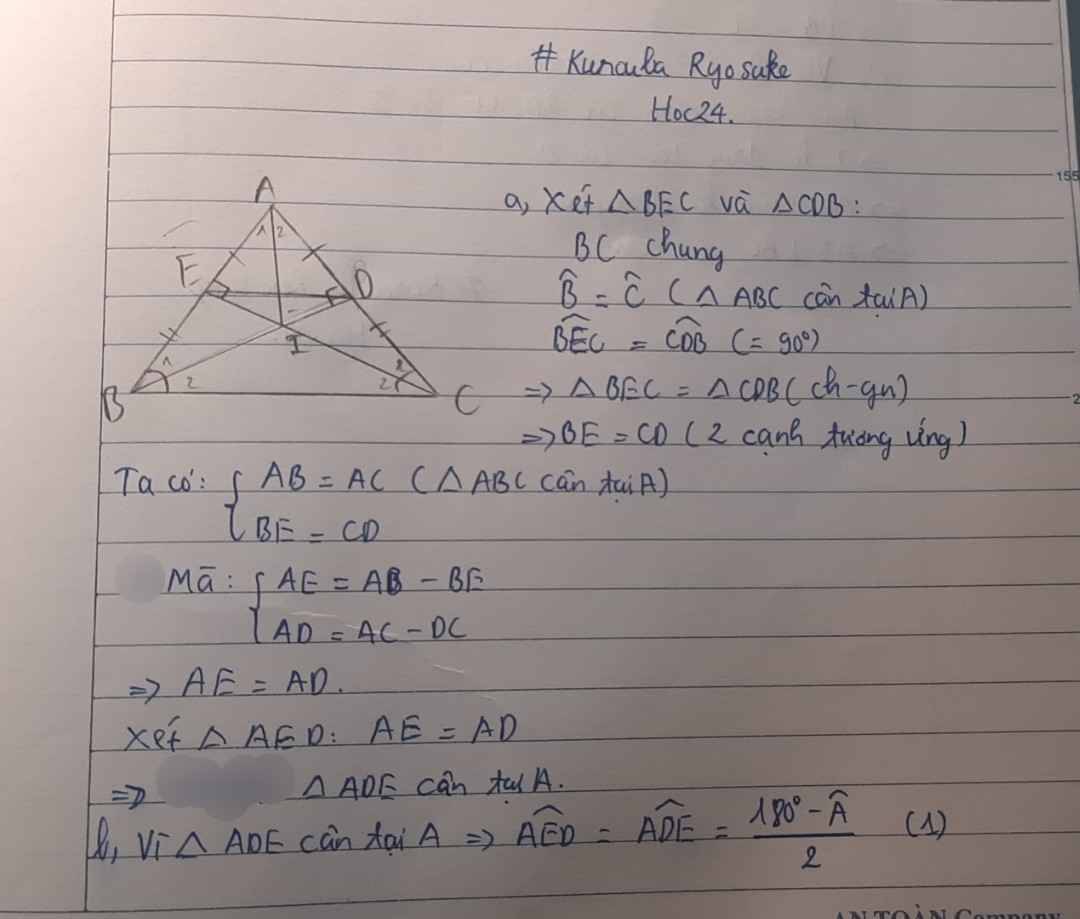

* câu d, í cậu, nếu cậu chưa học về các đường và t/c của tam giác cân với các đường đó thì bảo mk để mk làm lại cách khác cho nha :vv.
Đúng 3
Bình luận (2)
Cho ΔABC vuông tại A có AB=6,AC=8,đường cao AH, phân giác BD
a, Tính AH và BD
b, Gọi I là giao điểm AH và BD, DE vuông góc với BC. Cm AH/AC = HE/EC
cho đoạn thẳng BD và EC cắc nhau tại A cho AB = AC, AD= AE, AB \(\ge\) AD khẳng định nào sau đây sai
A. ΔABE = ΔACD B. ΔABC = ΔADC
C.\(\widehat{ABE}\) =\(\widehat{ACD}\) D. BE =CD
Cho ΔABC cân tại A. Vẽ phân giác BD,CE.
a) Chứng minh: BD=CE
b) Chứng minh DE=BC
c) Biết AB=AC=6cm, BC=4cm. Tính AD, DC
Cho ΔABC (AB<AC). Lấy D thuộc AB, E thuộc AC sao cho BD=CE. Đường thẳng MN cắt AB, AC tại I, K. Chứng minh ΔAIK cân
Cho ΔABC. Lấy điểm M bất kì nằm trong ΔABC. Kẻ MD, ME, MF lần lượt vuông góc với BC, AC, AB tại D, E, F. Chứng minh rằng AF^2 + BD^2 + EC^2 = AE^2 + FB^2 + DC^2.
ΔABC cân tại A (góc A <90 độ) BD vuông góc AC và CE vuông góc AB (D,EϵAC, AB). BD cắt CE = {H}
a) ΔABD=ΔACE
b) ΔBHC cân
c) ED // BC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
=>ΔADB=ΔAEC
b: góc ABD+góc HBC=góc ABC
góc ACE+gócHCB=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc HBC=góc HCB
=>ΔHBC cân tạiH
c: Xet ΔBAC có AE/AB=AD/AC
nên ED//BC
Đúng 1
Bình luận (0)
`a,`
Xét Tam giác `ABD` và Tam giác `ACE` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat{A} \) \(\text {chung}\)
`=> \text {Tam giác ABD = Tam giác ACE (ch-gn)}`
`b,`
Vì Tam giác `ABD =` Tam giác `ACE (a)`
`-> AD = AE (\text {2 cạnh tương ứng})`
`->`\(\widehat{ABD}=\widehat{ACE} (\text {2 góc tương ứng})\)
Ta có: \(\left\{{}\begin{matrix}AB=AE+BE\\AC=AD+DC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AD=AE\left(CMT\right)\end{matrix}\right.\)
`-> BE = DC`
Xét Tam giác `HEB` và Tam giác `HDC` có:
\(\widehat{HBE}=\widehat{HCD} (CMT)\)
`BE = DC (CMT)`
\(\widehat{HEB}=\widehat{CDH}=90^0\)
`=> \text {Tam giác HEB = Tam giác HDC}`
`-> HB = HC (\text {2 cạnh tương ứng})`
Xét Tam giác `BHC: HB = HC`
`->` Tam giác `BHC` cân tại `H`
`c,`
Xét Tam giác `AED: AE = AD (CMT)`
`-> \text {Tam giác AED cân tại A}`
`->`\(\widehat{AED}=\widehat{ADE} =\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A:`
`->`\(\widehat{ACB}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AED}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {ED = BC (đpcm)}.`

Đúng 2
Bình luận (0)




















