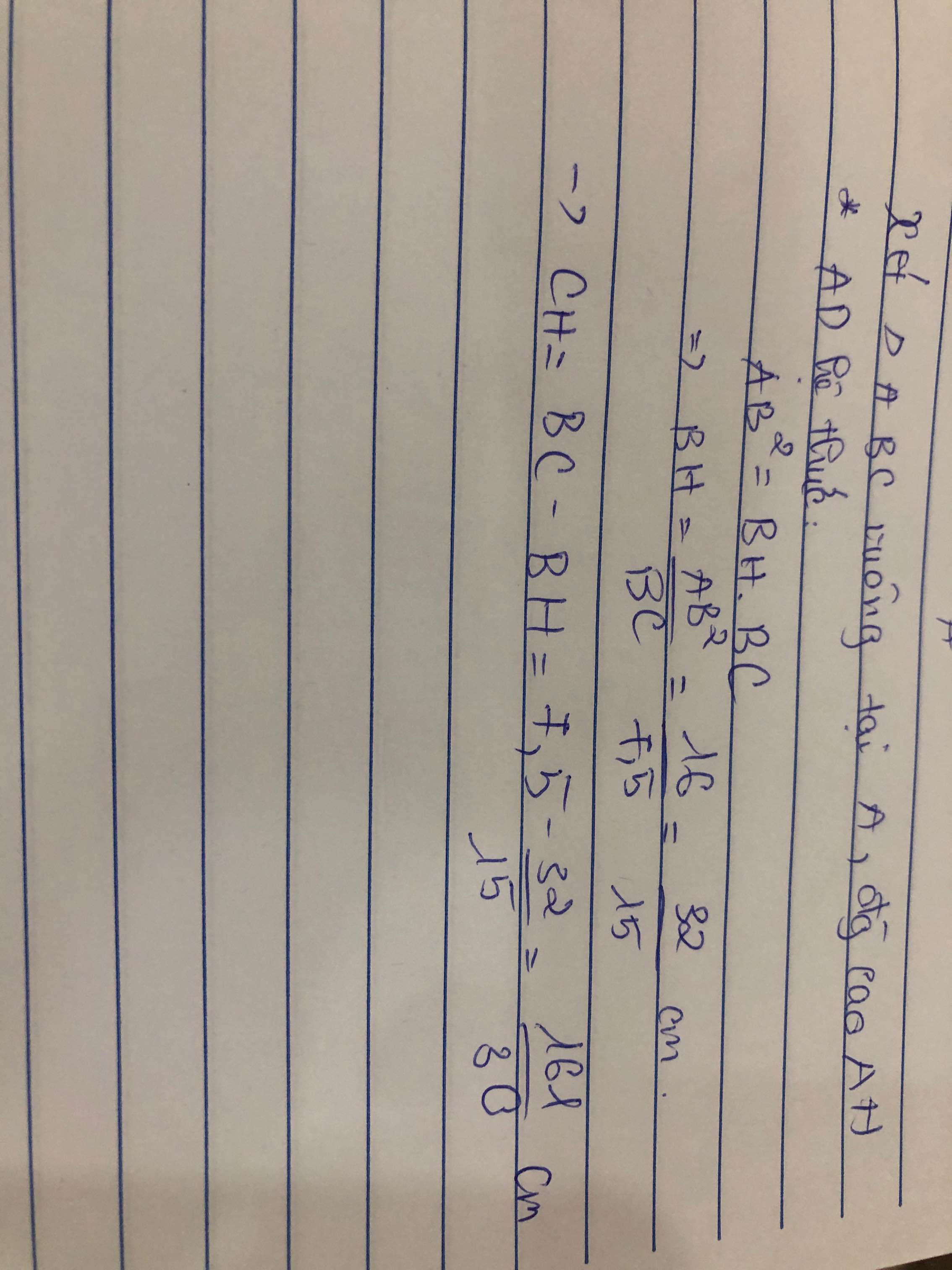cho tam giác ABC vuông tại A. Đường cao AH. Biết AB = 7,5 cm; AH =6cm . Tính AC; BC ; cos B ; cos C

Những câu hỏi liên quan
cho tam giác ABC vuông tại A đường cao AH , biết AB = 4 cm ,AC = 7,5 cm . Tính các cạnh các góc và đừờng cao AH trun g tuyến AM của tam giác ABC
Cho tam giác ABC vuông tại A kẻ đường cao AH. Biết AB=4cm, AC=7,5 cm. Tính HB,HC
TK:
Ta có tam giác vuông ABC với đường cao AH.
Theo định nghĩa, đường cao AH là đoạn thẳng vuông góc với cạnh đối diện và đi qua đỉnh của tam giác.
Vì tam giác ABC vuông tại A, nên AH là đường cao của tam giác.
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
\(AB^2+AC^2=BC^2\)
\(4^2+7,5^2=BC^2\)
\(16+56,25=BC^2\)
\(72,25=BC^2\)
\(BC\approx8,5cm\)
Vì AH là đường cao của tam giác ABC, nên AH chia BC thành hai đoạn HB và HC.
\(HB=BC\times\left(\dfrac{AB}{AC}\right)\)
\(HB=8,5\times\left(\dfrac{4}{7,5}\right)\)
\(HB\approx4,53cm\)
\(HC=BC-HB\)
\(HC=8,5-4,53\)
\(HC\approx3,97cm\)
Vậy \(HB\approx4,53cm\) và \(HC\approx3,97cm\)
Đúng 0
Bình luận (0)
Cho Tam giác ABC vuông tại A , đường cao AH . Cho biết AB = 4 cm , BC = 7,5 cm . Tính độ dài các đoạn thẳng BH ,HC
Cho tam giác Abc vuông tại A nội tiếp đường tròn tâm O có AB=7,5 cm, đường cao AH=4,5 cm.Tính R của đường tròn tâm O
Vì ΔABC vuông tại A nội tiếp \(\left(O\right)\) nên O là trung điểm của BC
hay R=OB=OC
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=7.5^2-4.5^2=36\)
hay HB=6cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BC=\dfrac{7.5^2}{6}=9.375\left(cm\right)\)
\(\Leftrightarrow R=4.6875\left(cm\right)\)
Đúng 0
Bình luận (0)
giúp mik bài này với
1, Cho tam giác ABC vuông tại A, p/g AD, đường cao AH. Biết BH= 7,5 cm, CD= 10 cm. Tính AH, AD
Sửa đề: BD=7,5cm
BC=7,5+10=17,5cm
AD là phân giác
=>AB/BD=aC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=17,5^2
=>k=3,5
=>AB=10,5cm; AC=14cm
AH=10,5*14/17,5=8,4cm
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos45=\dfrac{2\cdot10.5\cdot14}{10.5+14}\cdot\dfrac{\sqrt{2}}{2}=6\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
B1:Cho tam giác Abc có BC=7,5 cm;CA=4,5 cm;AB=6 cm.Tam giacs Abc là tam giác j?Tính đường cao AH của tam giác abc,biết HB=4,8 cm
B2:Cho hình vuông ABCD có độ dài cạnh bằng 4 cm,1 đường thẳng đi qua C cắt cạnh AD tại K.Biết CK=5 cm.Tính chiều cao BH của tam giác BKC
B4:Cho tam giác Abc đều có cạnh là 6 cm
a)Kẻ đường cao AH.Tính AH?
b)Tính diện tích tam giác Abc?
Cho ABC có AB =6 cm, AC =4,5 cm BC = 7,5 cm
a. Chứng minh tam giác ABC vuông tại A
b.Tính các góc B,C và đường cao AH của tam giác
c.tính diện tích của tam giác ABC
\(a,BC^2=AB^2+AC^2\Rightarrow\Delta ABC\) vuông tại A
\(b,\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\\ AH=\dfrac{AB\cdot AC}{BC}=3,6\left(cm\right)\\ c,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot6\cdot4,5=13,5\)
Đúng 2
Bình luận (1)
a. \(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}=53^0\\sinB=\dfrac{AC}{BC}\approx37^0\end{matrix}\right.\)
\(\Rightarrow A=180^0-\left(C+B\right)=180^0-\left(53^0+37^0\right)=90^0\left(tong3goctrong1tg\right)\)
Vậy tg ABC vuông tại A
Đúng 1
Bình luận (1)
a. cm △ABC ⊥ tại A:
Xét: 62 + 4,52 = 7,52
=> AB2 + AC2 = BC2
=> △ABC ⊥ tại A ( Pi-ta-go đảo)
b. sinB= AC/BC
=> sinB= 4,5/7,5 = 0,6
=>∠B = 38,87
góc C tương tự nhé!
Xét △ABC vuông tại A, đường cao AH:
=> 1/AB2 + 1/AC2 = 1/AH2 ( hệ thức lượng)
=> 1/62 + 1/4,52 = 1/AH2
AH = 3,6 ( cm)
c. S△ABC= \(\dfrac{AB.AC}{2}\)
= \(\dfrac{6.4,5}{2}\)
= 13,5 ( cm2)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6 cm ; AC = 4,5 cm ; BC = 7,5 cm a) chứng minh tam giác ABC vuông tại A b) Kẻ đường cao AH (H thuộc BC) tính BH, HC, AH và góc B,C của tam giác c) Tính diện tích tam giác ABC d) tìm vị trí điểm M để diện tích tam giác ABC bằng diện tích tam giác MBC
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
Đúng 0
Bình luận (0)