1. Tìm m , n để có :
a. { x \(\in\) R / x2 - mx + n = 0 } = { 1 ; 2 }
b. { x \(\in\) R / x3 - mx2 + nx - 2 = 0 } = { 1 ; 2 }
Tìm m để (m + 1) x 2 + mx + m < 0, ∀x ∈ R?
A. m < -1
B. m > -1
C. m < - 4 3
D. m > 4 3
Đáp án C
Bất phương trình (m + 1) x 2 + mx + m < 0, ∀x ∈ R khi và chỉ khi:
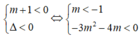
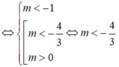
tìm 2 số thực m, n để có {x \(\epsilon\)R/ x2 -mx+n=0} ={1;2}
tìm 2 số thực m, n để có {x \(\varepsilon\)R/ x3 -mx2 +nx -2 =0}= {1; 2}
1.
Để $\left\{x\in\mathbb{R}|x^2-mx+n=0\right\}=\left\{1;2\right\}$ thì $x^2-mx+n=0$ có nghiệm $x=1$ và $x=2$Điều này xảy ra khi:
\(\left\{\begin{matrix} 1-m+n=0\\ 4-2m+n=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=3\\ n=2\end{matrix}\right.\)
2.
Để $\left\{x\in\mathbb{R}|x^3-mx^2+nx-2=0\right\}=\left\{1;2\right\}$ thì pt $x^3-mx^2+nx-2=0$ chỉ có 2 nghiệm $x=1$ và $x=2$Điều này xảy ra khi:
$x^3-mx^2+nx-2=(x-1)^2(x-2)$ (chọn) hoặc $x^3-mx^2+nx-2=(x-1)(x-2)^2$ (loại)
$\Leftrightarrow x^3-mx^2+nx-2=x^3-4x^2+5x-2$
$\Rightarrow m=4; n=5$
Cho A ={ x ∈ R | | m x − 3 | = m x − 3 } , B = { x ∈ R | x 2 − 4 = 0 }. Tìm m để B∖A=B
A. − 3 2 ≤ m ≤ 3 2
B. 0 < m < 3 2 hoặc − 3 2 < m < 0
C. − 3 2 < m < 3 2
D. m ≥ − 3 2
cho A={x\(\in\)R| |mx-3|=mx-3}, B={x\(\in\)R| \(x^2\)-4=0}. Tìm m để B\A=B
Trước tiên, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Tập A chứa các giá trị x thỏa mãn |mx-3|=mx-3. Điều này có nghĩa là ta cần tìm các giá trị x mà khi thay vào phương trình trên, phương trình vẫn đúng.
Tiếp theo, ta xác định tập hợp B: B là tập hợp các giá trị x thỏa mãn x^2-2x-4=0. Để giải phương trình này, ta có thể sử dụng công thức nghiệm của phương trình bậc 2, hoặc sử dụng định lý Viết.
Giải phương trình x^2-2x-4=0 bằng cách sử dụng công thức nghiệm của phương trình bậc 2, ta có: x = (2 ± √(2^2 - 41(-4))) / (2*1) = (2 ± √(4 + 16)) / 2 = (2 ± √20) / 2 = 1 ± √5
Vậy tập hợp B là B = {1 + √5, 1 - √5}.
Cuối cùng, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Điều này có nghĩa là ta cần loại bỏ các giá trị x thuộc tập A khỏi tập B.
Từ phương trình |mx-3|=mx-3, ta có hai trường hợp để xác định tập A:
Khi mx-3 > 0, ta có mx-3 = mx-3, điều này đúng với mọi giá trị x.Khi mx-3 < 0, ta có -(mx-3) = mx-3, điều này đúng khi mx > 3.Với mọi giá trị x thỏa mãn mx > 3, ta có x thuộc tập A.
Vậy tập hợp B\A = B - A = {1 + √5, 1 - √5} - {x | mx > 3}.
Để tìm m sao cho B\A = B, ta cần tìm giá trị m mà tập hợp B\A bằng tập hợp B. Tức là, ta cần giải phương trình sau: {1 + √5, 1 - √5} - {x | mx > 3} = {1 + √5, 1 - √5}.
Điều này xảy ra khi và chỉ khi tập hợp {x | mx > 3} không chứa bất kỳ giá trị nào từ tập hợp {1 + √5, 1 - √5}. Nghĩa là không có giá trị x thỏa mãn mx > 3 và x thuộc {1 + √5, 1 - √5}.
Vì vậy, để B\A = B, ta cần tìm giá trị m sao cho không có giá trị x thuộc {1 + √5, 1 - √5} thỏa mãn mx > 3.
Tuy nhiên, không có giá trị m nào thỏa mãn yêu cầu trên vì tập hợp {1 + √5, 1 - √5} chứa cả hai giá trị x lớn hơn 3 và nhỏ hơn 3.
Vậy không tồn tại giá trị m để B\A = B.
Cho hs
\(f\left(x\right)=-\dfrac{mx^3}{3}+3x^2-mx+1\)
tìm m để
a) \(f'\left(x\right)\le0,\forall x\in R\)
b) pt\(f'\left(x\right)=0\) có 2 nghiệm âm phân biệt
Tìm m để hai phương trình x 2 + m x + 1 = 0 v à x 2 + x + m = 0 có ít nhất một nghiệm chung
A. 1
B. 2
C. −1
D. −2
Gọi x0 là nghiệm chung của hai phương trình
thì x0 phải thỏa mãn hai phương trình trên:
Thay x = x0 vào hai phương trình trên ta được
x 0 2 + m x 0 + 1 = 0 x 0 2 + x 0 + m = 0
⇒ (m – 1)x0 + 1 – m = 0
⇔ (m – 1)(x0 – 1) = 0 (*)
Xét phương trình (*)
Nếu m = 1 thì 0 = 0 (luôn đúng)
hay hai phương trình trùng nhau
Lúc này phương trình x2 + x + 1 = 0
vô nghiệm nên cả hai phương trình đều vô nghiệm.
Vậy m = 1 không thỏa mãn.
+) Nếu m ≠ 1 thì x0 = 1
Thay x0 = 1 vào phương trình x02 + mx0 + 1 = 0 ta được m = −2
Thay m = −2 thì hai phương trình có nghiệm chung
Đáp án cần chọn là: D
a, trong mặt phẳng tọa độ oxy cho đường thẳng : y= mx +n ( d) đi qua điểm m -5 ; 3 ) và điểm n (-3;5) .tìm m,n ?
b, cho phương trình : x2 -4nx + 12n -9 = 0 ( 1) ( m là tham số ) . tìm các giá trị của n để phương trình (1) có hai nghiệm x1 , x2 thỏa mãn đẳng thức : x1(x2+ 3 ) + x2(x1+ 3) -54 =0
( giải giúp mình bt này với ạ)
Cho A =\(\left\{x\in R|\left|mx-3\right|=mx-3\right\}\) , B=\(\left\{x\in R|x^2-4=0\right\}\).Tìm m để B\A = B
\(\left|mx-3\right|=mx-3\Leftrightarrow mx-3\ge0\) \(\Rightarrow\left[{}\begin{matrix}x\ge\dfrac{3}{m}\left(m>0\right)\\x\le\dfrac{3}{m}\left(m< 0\right)\end{matrix}\right.\)
\(x^2-4=0\Rightarrow x=\pm2\Rightarrow B=\left\{-2;2\right\}\)
\(B\backslash A=B\Leftrightarrow A\cap B=\varnothing\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{3}{m}>2\left(m>0\right)\\\dfrac{3}{m}< -2\left(m< 0\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}0< m< \dfrac{3}{2}\\-\dfrac{3}{2}< m< 0\end{matrix}\right.\)
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3