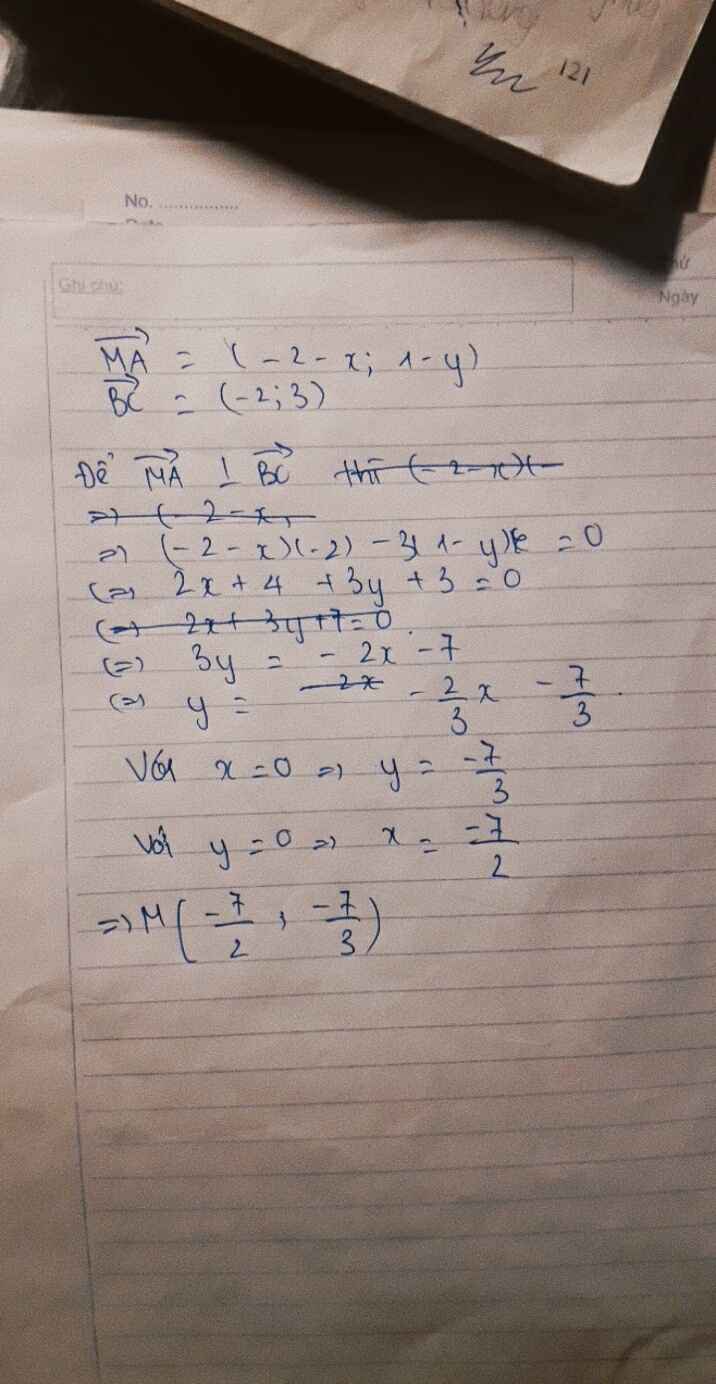Mn giúp mình với ạ Trong mặt phẳng toạ độ có điểm M (1; -2) thuộc đồ thị hàm số y= ax². a, Tìm hệ số a. b, vẽ đồ thị hàm số vừa tìm được

Những câu hỏi liên quan
Giúp mình với ạ, mình cảm ơn !
Trong mặt phẳng toạ độ Oxy cho điểm M nằm trên trục hoành có hoành độ bằng -1, toạ độ của điểm M là:
A. M(0;-1)
B. M(-1;0)
C. M(-1;-1)
D. M(-1;1)
Trên mặt phẳng toạ độ Oxy, cho A(1;1), B(2:-2), M thuộc Oy và MA=MB. Khi đó toạ độ điểm M(a,b). Tính a + b.
Giải giúp mình với ạ, mình cảm ơn.
Xem chi tiết
Ta có: \(M\left( {0;y} \right)\)
Lại có: \(\overrightarrow {MA} \left( {1;1 - y} \right),\overrightarrow {MB} \left( {2; - 2 - y} \right)\)
Theo yêu cầu bài toán, suy ra: \({1^2} + {\left( {1 - y} \right)^2} = {2^2} + {\left( {2 + y} \right)^2} \Leftrightarrow 1 + 1 - 2y + {y^2} = 4 + 4 + 4y + {y^2} \Leftrightarrow y = - 1\)
Nên \(M\left( {0; - 1} \right)\)
Vậy \(a = 0,b = - 1 \Rightarrow a + b = 0 + \left( { - 1} \right) = - 1\)
Đúng 2
Bình luận (0)
1. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng △ song song với đường thẳng d: 2x-y+2015=0 và cắt hai trục toạ độ tại M và N sao cho MN=3√5
2.Trong mặt phẳng với hệ toạ độ Oxy, cho 2 điểm A(1;2) ; B(4;3). Tìm toạ độ điểm M sao cho ∠MAB=135 độ và khoảng cách từ M đến đường thẳng AB bằng √10/2
Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Đúng 0
Bình luận (0)
Bài 1 cho hàm số y=3x² có đồ thị (P) và đường thẳng (d) : y=2x+1 a,vẽ đồ thị hàm số y=3x² trên mặt phẳng toạ độ b,tìm toạ độ giao điểm của (P)và (d) bằng phép tính Mong mn giải giúp ạ
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)
Đúng 0
Bình luận (0)
Câu 2 a)Vẽ F(2;3) trong mặt phẳng toạ độ Oxy và điểm K(-1,4) b)Cho ∆ABC có C=32° ,B=45° Tính góc A c) ∆ABC là tam giác gì? Giúp mình với ạ😊👉❤️👈
Giúp em bài này với ạ:
Câu 16: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1;-2) ; B(3;2). Tìm điểm M sao cho B là trung điểm của đoạn thẳng AM
A. M(5;6)
B. M(2;0)
C. M(4;0)
D. M(-1;-6)
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Đúng 0
Bình luận (0)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho các điểm A(-2;1), B(4;0), C(2;3). Tìm điểm M thuộc trục Oy sao cho MA vuông góc với BC Giải chi tiết giúp e với ạ e đang cần gấp ạ
Trong mặt phẳng toạ độ Oxy, cho hai điểm M(1/3;1/2), N(4/3;5/2). Tìm toạ độ giao điểm I của MN và trục Oy
Gọi ptđt MN là y= ax+b (d)
Vì \(M,N\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}\frac{1}{3}a+b=\frac{1}{2}\\\frac{4}{3}a+b=\frac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-\frac{1}{6}\end{matrix}\right.\Rightarrow y=2x-\frac{1}{6}\)
PTHĐGĐ:
\(2.0-\frac{1}{6}=y\Rightarrow y=-\frac{1}{6}\)
Vậy \(I\left(0;-\frac{1}{6}\right)\)
#2H3Y1-1~Trong không gian với hệ toạ độ Oxyz, hình chiếu của điểm M(1;-3;-5) trên mặt phẳng (Oyz) có toạ độ là: A. (0;-3;0) B. (0;-3;-5) C. (0;-3;5) D. (1;-3;0).
Đọc tiếp
#2H3Y1-1~Trong không gian với hệ toạ độ Oxyz, hình chiếu của điểm M(1;-3;-5) trên mặt phẳng (Oyz) có toạ độ là:
A. (0;-3;0)
B. (0;-3;-5)
C. (0;-3;5)
D. (1;-3;0).
Đáp án B
Phương trình mặt phẳng (Oyz) là x=0 và hình chiếu của điểm I(a;b;c) lên mặt phẳng (Oyz) là (0;b;c).
Đúng 0
Bình luận (0)