Cho tam giác ABC cân tại A, có B=2A. Vẽ \(AH\perp CD\left(H\in BC\right);BK\perp AC\left(K\in AC\right)\). AH cắt BK tại M. Nối M với C
a) C/m: Tam giác MBC cân
b) Vẽ Bx//MC và cắt AH kéo dài tại N. CMR: HM=HN
c) CMR: tam giác BAN vuông
Câu 1 : Cho tam giác ABC đều . Kẻ \(AH\perp BC\left(H\in BC\right)\). TIa phân giác của góc ACB cắt AH tại E . Vẽ \(EK\perp AC\left(K\in AC\right)\). Lấy I là trung điểm của AB . CMR :
a) tam giác EHC = tam giác EKC
b) tam giác CHK đều
c) tam giác AKH cân
d) Ba điểm C,E,I thẳng hàng
Câu 1 : Cho tam giác ABC đều . Kẻ \(AH\perp BC\left(H\in BC\right)\). TIa phân giác của góc ACB cắt AH tại E . Vẽ \(EK\perp AC\left(K\in AC\right)\). Lấy I là trung điểm của AB . CMR :
a) tam giác EHC = tam giác EKC
b) tam giác CHK đều
c) tam giác AKH cân
d) Ba điểm C,E,I thẳng hàng
Câu 1 : Cho tam giác ABC đều . Kẻ \(AH\perp BC\left(H\in BC\right)\). TIa phân giác của góc ACB cắt AH tại E . Vẽ \(EK\perp AC\left(K\in AC\right)\). Lấy I là trung điểm của AB . CMR :
a) tam giác EHC = tam giác EKC
b) tam giác CHK đều
c) tam giác AKH cân
d) Ba điểm C,E,I thẳng hàng
Cho tam giác ABC vuông tại A, AH\(\perp\)BC. Vẽ \(HD\perp AB\left(D\in AB\right),HE\perp AC\left(E\in AC\right)\). Biết BH =9cm, HC= 16cm. Tính DE
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=BH\cdot CH\)
\(\Leftrightarrow AH^2=9\cdot16=144\)
hay AH=12(cm)
Xét tứ giác ADHE có
\(\widehat{EAD}=90^0\)
\(\widehat{ADH}=90^0\)
\(\widehat{AEH}=90^0\)
Do đó: ADHE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AH=DE(Hai đường chéo)
mà AH=12(cm)
nên DE=12cm
Cho tam giác ABC vuông tại A có AB=15cm, AC=20cm. Vẽ \(AH\perp BC\) tại H.
a) Tính BC, AH
b) Vẽ BD là phân giác của \(\widehat{ABC}\left(D\in AC\right)\) Tính DC
c) Gọi I là giao điểm của AH và BD. Chứng minh AI.AD = IH.DC
d) Trên cạnh HC lấy E sao cho HE=HA, qua E vẽ đường thẳng \(\perp BC\) cắt AC ở M, qua C vẽ đường thẳng \(\perp BC\) cắt tia phân giác của \(\widehat{MEC}\) tại F. Chứng minh H,M,F thẳng hàng
Cho tam giác ABC cân tại A \(\left(\widehat{A}< 90^0\right)\). Vẽ \(BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right)\)
a) Chứng minh rằng AH = AK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là phân giác của góc A
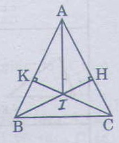
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)
Cho tam giác ABC vuông tại A có AB < AC . Vẽ \(AH\perp BC\left(H\in BC\right),D\)là điểm trên cạnh AC sao cho AD = AB. Vẽ \(DE\perp BC\left(E\in BC\right).\)Chứng minh rằng HA = HE
(lưu ý : vẽ thêm đường phụ)
△ABC" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> vuông tại A nên
⇒△MAB;△MAC" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> cùng cân tại M
⇒MD" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> vừa là đường cao, vừa là đường phân giác trong .
⇒△BMD=△AMD(c.g.c)⇒DBM^=DAM^=90∘→DB⊥BC" role="presentation" style="border:0px; direction:ltr; display:inline-table; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
△AME=△CME(c.g.c)→ECM^=MAE^=90∘→CE⊥BC" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
DB//CE" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
BD=DA;CE=AE→" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:16.38px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml"> đpcm
bẠN kham khỏa nhé.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB=a,SA\perp AB,SC\perp BC,SB=2a.\)Gọi \(M,N\) lần lượt là trung điểm \(SA,BC\). Gọi \(\alpha\) là góc giữa \(MN\) với \(\left(ABC\right)\) .Tính \(cos\alpha\).
Gọi D là hình chiếu vuông góc của S lên (ABC)
\(SD\perp\left(ABC\right)\Rightarrow SD\perp AB\) , mà \(AB\perp SA\left(gt\right)\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp AD\)
\(\Rightarrow AD||BC\)
Tương tự ta có: \(BC\perp\left(SCD\right)\Rightarrow BC\perp CD\Rightarrow CD||AB\)
\(\Rightarrow\) Tứ giác ABCD là hình vuông
\(\Rightarrow BD=a\sqrt{2}\)
\(SD=\sqrt{SB^2-BD^2}=a\sqrt{2}\)
Gọi P là trung điểm AD \(\Rightarrow MP\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MP=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\\MP||SD\Rightarrow MP\perp\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow\alpha=\widehat{MNP}\)
\(cos\alpha=\dfrac{NP}{MN}=\dfrac{NP}{\sqrt{NP^2+MP^2}}=\dfrac{a}{\sqrt{a^2+\dfrac{a^2}{2}}}=\dfrac{\sqrt{6}}{3}\)
Cho tam giác ABC cân tại A, vẽ AH \(\perp\) BC (H \(\in\) BC). Chứng minh rằng AH + BC > AB + AC.