Giúp mình câu 41 với ạ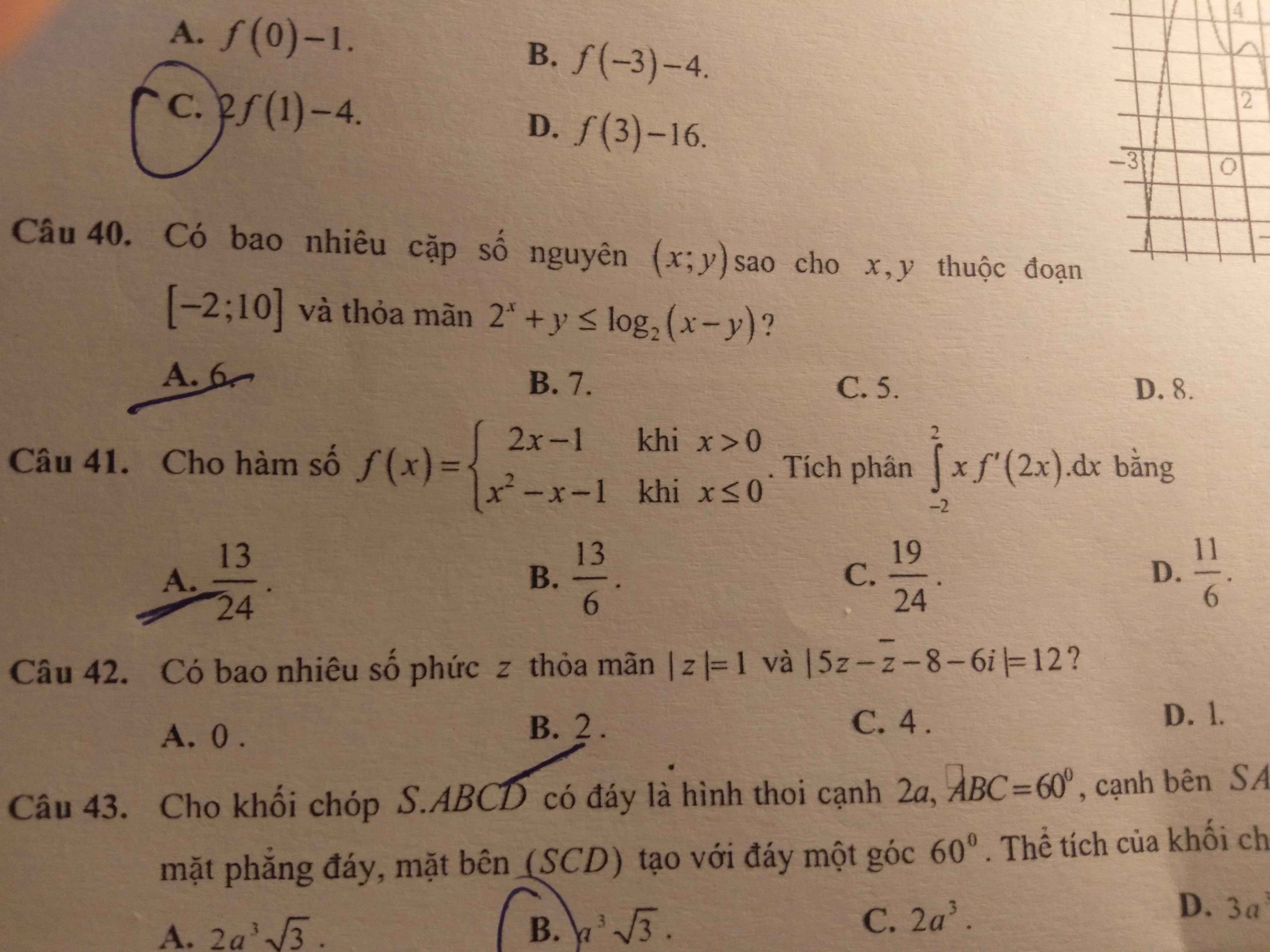

Những câu hỏi liên quan
GIÚP MÌNH CÂU 41 ĐẾN 51 VỚI Ạ
41 on
42 with/and
Tham khảo vế 1 c42
43 for
44 of
45 to
46 on
47 with
48 of
49 from
50 of
Đúng 3
Bình luận (2)
GIÚP MÌNH TỪ CÂU 41 ĐẾN 45 VỚI Ạ!

41. Roger: " I don't believe it. " - Anita: " ..................... "
→ Đáp án: C. Neither do I
42. Jill : " Do you know Lisa's an excellent pianist ? - Maria: " ..................... "
→ Đáp án: B. Yes, she does
43. Karen: " ............... this word in English ? " - Betsy: " C-O-Z-Y "
→ Đáp án: B. How do you spell
44. Customer: " I think my change is wrong. " - Shop assistant: " ................... "
→ Đáp án: C. Sorry. I don't think I have any change
45. Mandy: " I've got a toothache. " - George: " ................. "
→ Đáp án: D. Why don't you see the dentist ?
Đúng 2
Bình luận (0)
Giúp mình câu 39, 40 và 41 nha. Hình ở bên dưới ạ.
a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
Đúng 2
Bình luận (1)
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)
Đúng 2
Bình luận (0)
40/
\(\sqrt{1+ax}.\sqrt[3]{1+bx}+\sqrt[4]{1+cx}-1=\left(\sqrt{1+ax}-1\right)+\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)+\sqrt{1+ax}.\sqrt[3]{1+bx}.\left(\sqrt[4]{1+cx}-1\right)\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}-1}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}.\sqrt[3]{1+bx}\left(\sqrt[4]{1+cx}-1\right)}{x}\)
\(I_1=\lim\limits_{x\rightarrow0}\dfrac{1+ax-1}{x\left(\sqrt{1+ax}+1\right)}=\dfrac{a}{\sqrt{1+ax}+1}=\dfrac{a}{2}\)
\(I_2=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(1+bx-1\right)}{x\left(\sqrt[3]{\left(1+bx\right)^2}+\sqrt[3]{1+bx}+1\right)}=\dfrac{b\sqrt{1+ax}}{\sqrt[3]{\left(1+bx\right)^2+\sqrt[3]{1+bx}+1}}=\dfrac{b}{3}\)
\(I_3=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\sqrt[3]{1+bx}\left(1+cx-1\right)}{x\left(\sqrt[4]{\left(1+cx\right)^3}+\sqrt[3]{\left(1+cx\right)^2}+\sqrt[3]{1+cx}+1\right)}=\dfrac{c}{4}\)
\(\Rightarrow L=\dfrac{a}{2}+\dfrac{b}{3}+\dfrac{c}{4}\)
P/s: Thông cảm mình đang đau đầu nên làm hơi lâu :b
Đúng 3
Bình luận (3)
Xem thêm câu trả lời
Giải giúp em câu 41 với ạ. Em cảm ơn.

Gọi V là thể tích khi quay phần giới hạn bởi \(y=\dfrac{1}{x}\) ; x=1, y=0; Ox quanh Ox
\(\Rightarrow V=V_1+V_2\)
\(V=\pi\int\limits^5_1\dfrac{1}{x^2}dx=\dfrac{4\pi}{5}\)
\(V_1=\pi\int\limits^k_1\dfrac{1}{x^2}dx=-\dfrac{\pi}{x}|^k_1=\pi-\dfrac{\pi}{k}\)
\(\Rightarrow V_2=V-V_1=\dfrac{4\pi}{5}-\pi+\dfrac{\pi}{k}=\dfrac{\pi}{k}-\dfrac{\pi}{5}\)
\(\Rightarrow\pi-\dfrac{\pi}{k}=2\left(\dfrac{\pi}{k}-\dfrac{\pi}{5}\right)\)
\(\Rightarrow k=\dfrac{15}{7}\)
Đúng 2
Bình luận (0)
Giúp mình câu 41 đến 45 với
Mọi người giúp mình với mk cần gấp ạ. Mọi ng hãy chỉ ra nhiệt độ tháng cao nhất Nhiệt độ thâng thấp nhất Biên độ nhiệt Lượng mưa tháng thấp nhất Lượng mưa tháng cao nhất Tổng lượng mưa CÂU 4 BÀI 12/41 Ạ
Xem thêm câu trả lời
GIÚP MÌNH TỪ CÂU 37 ĐẾN 41 VỚI

giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
chỉ giúp mình câu này với
e) 2/x-2 + 41 = 7/2
ĐỀ:
\(\dfrac{2}{x}-2+41=\dfrac{7}{2}\)
ĐÁP ÁN:
\(x=\dfrac{-4}{71}\)
Đúng 0
Bình luận (0)

























