Cho S=1+2+22+...+22005. Hãy so sánh S với 5.22004

Những câu hỏi liên quan
câu 1: không tính giá trị hãy so sánh hai số a, b sau đây
a = 2007.2009 b= 20082
câu 2 cho S = 1+ 2 + 22 + .... + 22005 hãy so sánh S với 5.22004
giúp e với ạ
gấp rút
ai gửi đầu tiên e tim cho
Đúng 0
Bình luận (0)
mik bt lm câu 1 thôi nha, bn thông cảm:
a = 2007.2009 b = 20082
=(2008 - 1)(2008 + 1)
= 20082 - 1
Ta có, a = 20082 - 1, b = 20082
mà 20082 - 1 < 20082
=> a < b
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho S=1+2+22+23+…+29 hãy so sánh S với 5.28
\(S=1+2+2^2+2^3+...+2^9\)
Đặt \(2S=2+2^2+2^3+2^4+...+2^{10}\)
\(2S-S=2^{10}-1\) hay \(S=2^{10}-1< 2^{10}\)
\(\Rightarrow\) \(2^{10}=2^2.2^8< 5.2^8\)
Vậy \(S< 5.2^8\)
\(#Tuyết\)
Đúng 3
Bình luận (1)
2S=2+2^2+...+2^10
=>S=2^10-1=1023
5*2^8=256*5=1280
=>S<5*2^8
Đúng 3
Bình luận (0)
`@` `\text {Answer}`
`\downarrow`
`S = 1 + 2 + 2^2 + 2^3 + ... + 2^9`
`=> 2S = 2 + 2^2 + 2^3 + ... + 2^10`
`=> 2S - S = (2+2^2 + 2^3 + ... + 2^10) - (1 + 2 + 2^2 + 2^3+...+2^9)`
`=> S = 2^10 - 1`
Mà `2^10 - 1 < 2^10`
`=> S < 2^10 (1)`
Ta có:
`2^10 = 2^7*8`
Mà `5*2^8 = 5* 2 * 2^7 = 10* 2^7`
Vì `10 > 8 => 2^7 * 8 < 2^7 * 10 (2)`
Từ `(1)` và `(2)`
`=> S < 5 * 2^7``.`
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Tính S= 1/22+1/23+...+1/22005
\(S=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2005}}\)
\(2.S=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(2.S-S=\left(2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(S=2-\dfrac{1}{2^{2006}}\)
Đúng 2
Bình luận (0)
Cho S = 1 phần 20 + 1 phần 21 + 1 phần 22 + 1 phần 29 . Hãy so sánh S với 1 phần 3
ta thấy \(\frac{1}{20}\)<\(\frac{1}{3}\)
thì \(\frac{1}{20}\)+...+\(\frac{1}{29}\)<\(\frac{1}{20}\)+...+\(\frac{1}{20}\)<\(\frac{1}{3}\)
vậy \(\frac{1}{20}\)+...+\(\frac{1}{29}\)<\(\frac{1}{3}\)
Đúng 0
Bình luận (0)
S =1 / 21 + 1/ 22 + 1/ 23 + ... + 1 / 149 + 1 / 150
hãy so sánh S với 3/ 4
Sửa đề: \(S=\dfrac{1}{20}+\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{50}\)
Ta có: \(S=\dfrac{1}{20}+\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{50}\)
\(=\dfrac{1}{20}+\left(\dfrac{1}{21}+\dfrac{1}{22}+...+\dfrac{1}{30}\right)+\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)\)
\(\Leftrightarrow S>\dfrac{1}{20}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{1}{4}+\dfrac{1}{3}+\dfrac{1}{4}\)
\(\Leftrightarrow S>\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{3}{4}\)(đpcm)
Đúng 0
Bình luận (1)
Có : \(S=1+2+2^2+2^3+....+2^{99}\)
\(\Rightarrow2S=2+2^2+2^3+....+2^{100}\)
\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{100}\right)-\left(1+2+2^2+....+2^{99}\right)\)
\(\Rightarrow S=2^{100}-1< 2^{100}\)
Vậy \(S< 2^{100}\)
Đúng 1
Bình luận (0)
S=1+2+22+23+....+299
⇒2S=2+22+23+....+2100
⇒2S−S=2100-1
S=2100-1
vì 2100 -1<2100
⇒S<2100
Đúng 1
Bình luận (0)
Xét tổng S gồm 20 số hạng:
S=1/1×2×3×4+1/2×3×4×5+...+1/20×21×22×23.
Hãy so sánh tổng S với 1/18
cậu ko giúp cậu ấy thì thôi đừng bảo như thế
Hãy so sánh S với 6/25
S=1/21+1/22+....+1/40
cần gấp nha ,thanks
1/21+1/22+....+1/40>1/40.20=1/2=6/12>6/25
=>S>6/25
Đúng 0
Bình luận (0)
có ai on ko,chat với tui ik
S=1+2+22+23+...+29. So sánh S với 5. 28
\(S=1+2+2^2+...+2^9\)
\(S=\dfrac{2^{9+1}-1}{2-1}\)
\(S=2^{10}-1=1023\)
\(5.2^8=5.256=1280>1023\)
\(\Rightarrow S< 5.2^8\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho S=1+2+2^2+....+2^2005.Hãy so sánh S với 5*2^2004
Giúp mình với,thanks
\(S=1+2+2^2+...+2^{2005}\\ 2S=2+2^2+...+2^{2006}\\ 2S-S=S=2^{2006}-1< 2^{2006}+2^{2004}=2^2\cdot2^{2004}+2^{2004}=5\cdot2^{2004}\)
Đúng 0
Bình luận (0)



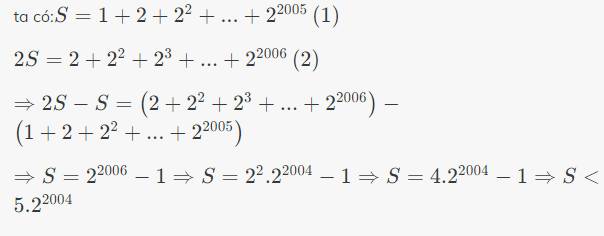 câu 2 nè nha bn
câu 2 nè nha bn






























