cho tam giác tìm điểm k sao cho vecto ka + 2 kb = cb tìm điểm m sao cho vec ma + mb + 2mc = 0

Những câu hỏi liên quan
cho tam giác ABC
tìm điểm O sao cho : vecto OA+vecto OB+vecto OC= vecto 0
tìm điểm K sao cho : vecto KA+2 vecto KB= vecto CB
tìm điểm M sao cho : vecto MA+ vecto MB+ 2 vecto MC = vecto 0
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)⇒ O là trọng tâm tam giác ABC
\(\overrightarrow{K\text{A}}+2\overrightarrow{KB}=\overrightarrow{CB}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KB}+\overrightarrow{BC}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KC}=\overrightarrow{0}\)
⇒ K là trọng tâm tam giác ABC
Câu cuối chịu :))
Đúng 0
Bình luận (0)
Cho tam giác ABC
a) Tìm điểm K sao cho \(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
b) Tìm điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\)
a)Giả sử điểm K thỏa mãn:
\(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)\(\Leftrightarrow\overrightarrow{KB}+\overrightarrow{BA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
\(\Leftrightarrow3\overrightarrow{KB}=\overrightarrow{CB}-\overrightarrow{BA}\)
\(\Leftrightarrow\overrightarrow{KB}=\overrightarrow{CB}+\overrightarrow{AB}\).
Xác định: \(\overrightarrow{CB}+\overrightarrow{AB}\).
Lấy điểm D sao cho B là trung điểm của DC.
\(\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{BD}+\overrightarrow{AB}=\overrightarrow{AD}\).
Điểm K xác định sao cho : \(\overrightarrow{KB}=\overrightarrow{AD}\) hay tứ giác AKBD là hình bình hành.
Đúng 0
Bình luận (1)
b) Gọi G là trọng tâm tam giác ABC.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\overrightarrow{MG}\)\(+2\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\overrightarrow{GC}\).
Giả sử điểm M thỏa mãn:
\(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow4\overrightarrow{MG}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
Điểm M được xác định để \(\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
Gọi T là trung điểm của AB nên \(\overrightarrow{CG}=2\overrightarrow{GT}\).
Vì vậy điểm M được xác định là trung điểm của GT.
Đúng 0
Bình luận (0)
: Cho tam giác ABC Xác định điểm K sao cho veto ka + 3 vecto kb - 2 vecto kc = vecto 0
Cho hình vuông ABCD cạnh a a) xác định điểm K thỏa mãn vecto KA+ vecto KB+ vecto KC+4vecto KD = vecto 0 b) tìm {M} thỏa mãn : | vecto MA+ vecto MB + vecto MC +4vecto MF| = 2a c) tìm {N} thỏa mãn : |2 vecto NA- vecto NB + vecto NC | = | vecto ND +vecto NC|
mn ơi giúp mik bài này với , mik đang cần gấp
cho tam giác ABC
a. tìm điểm I sao cho 2 vec tơ IB 2 vec tơ IB + 3 vec tơ IC vec tơ 0
b. tìm điểm J sao cho vec tơ JA - vec tơ JB - 2 vec tơ JC vec tơ 0
c. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC vec tơ BC
d. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC 2 vec tơ BC
e. tìm điểm L sao cho 3 vec tơ LA - vec tơ LB + 2 vec tơ LC vec tơ 0
Đọc tiếp
mn ơi giúp mik bài này với , mik đang cần gấp
cho tam giác ABC
a. tìm điểm I sao cho 2 vec tơ IB 2 vec tơ IB + 3 vec tơ IC = vec tơ 0
b. tìm điểm J sao cho vec tơ JA - vec tơ JB - 2 vec tơ JC = vec tơ 0
c. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC = vec tơ BC
d. tìm điểm K sao cho vec tơ KA + vec tơ KB + vec tơ KC = 2 vec tơ BC
e. tìm điểm L sao cho 3 vec tơ LA - vec tơ LB + 2 vec tơ LC = vec tơ 0
1/ Cho hình bình hành ABCD tâm O
Chứng minh véctơ MA + MB + MC = véctơ 0
2/ Cho tứ giác ABCD. I, J là trung điểm của AC, BD
Chứng minh véc tơ AB + CD = 2 véctơ IJ
3/ Cho tam gian giác ABC
a) Tìm điểm K sao cho véctơ KA + 2KB = véctơ CB
b) Tìm điểm M sao cho véctơ MA + MB + 2MC = véctơ 0
1)
MA → MA → +MB → MB → +MC → MC → +MD → MD →
=4MO → MO → +(OA → OA → +OC → OC → )+(OB → OB → +OD → OD → )
=4MO →
2) chèn điểm IJ vào AB+CD nhé!
=>AI+IJ+JB+CI+IJ+JD
=2IJ+(AI+CI)+(JB+JD)
=2IJ + O + O(vì I,J là trung điểm của AC và BD)
=2IJ(đpcm)
Đúng 0
Bình luận (0)
3)
a.vectơ KA + 2KB = CB (1)
Lấy N trên AB sao cho vectơNA + 2NB = 0 (hay tỉ lệ đoạn thẳng MA/MB = 2)
=> vectơKA - KN + (2KB - 2KN) = 0
=> vectơKA + 2KB = 3KN(2)
(1),(2) => vectơ CB = 3KN
Từ đó suy ra cách xác định điểm K.
b. vectơ MA + MB + 2MC = 0
=>vectơ MA + MA + AB + 2MA + 2AC = 0
=>vectơ 4MA = -(AB + 2AC) (3)
Trên đoạn BC dựng điểm P sao cho PB + 2PC = 0 (hay tỉ lệ đoạn PB/PC = 2)
=> AB - AP + 2AC - 2AP = 0
=> AB + 2AC = 3AP (4)
(3),(4) => vectơ 4MA = 3PA
Từ đó suy ra cách xác định điểm K.
Đúng 0
Bình luận (0)
Cho tam giác ABC và đường thẳng d a) tìm điểm I để Vecto IA+IB+3IC =vecto 0. b) Tìm trên d điểm M sao cho |Vecto MA+MB+3MC| nhỏ nhất giúp mk với mk đang cần gấp !!!
a) Gọi E là trung điểm AB \(\Rightarrow\) \(\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IE}\)
\(\overrightarrow{IA}+\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(2\overrightarrow{IE}+3\overrightarrow{IC}=\overrightarrow{0}\)
b) \(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}+3\overrightarrow{MI}+3\overrightarrow{IC}\right|\)
\(=5MI\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|min\Leftrightarrow MImin\)
\(\Leftrightarrow\) M là hình chiếu của I trên d
Đúng 2
Bình luận (0)
Cho tam giác ABC.Tìm tập hợp điểm M sao cho /vecto MA+3MB-2MC/ =/2MA-MB-MC/
Cho tam giác ABC. Tìm điểm M thỏa mãn
M
A
→
+
M
B
→
+
2
M
C
→
0
→
A. M là trung điểm cạnh IC , với I là trung điểm của cạnh AB B. M trùng với đỉnh C của tam giác ABC C. M là trọng tâm của tam giác ABC. D. M là đỉnh của hình...
Đọc tiếp
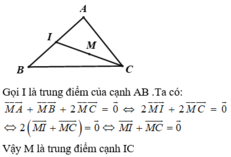
Cho tam giác ABC. Tìm điểm M thỏa mãn M A → + M B → + 2 M C → = 0 →
A. M là trung điểm cạnh IC , với I là trung điểm của cạnh AB
B. M trùng với đỉnh C của tam giác ABC
C. M là trọng tâm của tam giác ABC.
D. M là đỉnh của hình bình hành MCAB
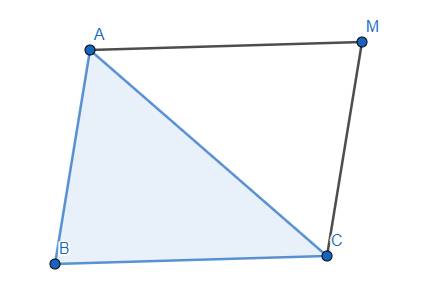
Cho tam giác ABC Xác định vị trí điểm M sao cho vecto MA - vecto MB + vecto MC = vecto 0
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
Đúng 1
Bình luận (0)