Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat{BAH}=\widehat{OAC}\).

Những câu hỏi liên quan
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H $\in$ BC). Chứng minh rằng $\widehat{BAH}=\widehat{OAC}$.
Vẽ đường kính AK
+) Dễ có: ^KBC = ^KAC (2 góc nội tiếp cùng chắn cung KC) (1)
+) ^ABK là góc nội tiếp chắn nửa đường tròn nên ^ABK = 900
Có: ^KBC + ^CBA = ^ABK = 900 (cmt)
^BAH + ^CBA = 900 (∆ABH vuông tại H)
Từ đó suy ra ^KBC = ^BAH (2)
Từ (1) và (2) suy ra ^BAH = ^KAC hay ^BAH = ^OAC (đpcm)
Kẻ đường kính AE của đường tròn ( O) . Ta thấy \(\widehat{ACE}=90^o\)( góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{OAC}+\widehat{AEC}=90^o\) (1)
Theo gt, ta có: \(\widehat{BAH}+\widehat{ABC}=90^O\) (2)
Lại có: \(\widehat{AEC}=\widehat{ABC}\) (3)
Từ (1), (2), (3) => đpcm
có AEC = ABC ( góc nội tiếp chắn cung AC)
mà AHB = AEC ( =90 độ )
nên tam giác ABH ~ tam giác AEC
=> BAH = EAC=OAC
Xem thêm câu trả lời
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. AH kéo dài cắt đường tròn (O;R) tại D:
a, Chứng minh rằng\(\widehat{BAH}=\widehat{CAO}\)
b, Giả sử AH=R. Chứng minh rằng: \(\widehat{BAC}=60^o\)
c, Tính tổng: \(^{AB^2+BD^2+DC^2+CA^2}\)theo R
cho tam giác ABC nội tiếp đường tròn , kẻ đường cao AH của tam giác và đường kính AD của đường tròn . Chứng ,minh rằng \(\widehat{BAH}=\widehat{DAC}\)
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{ABH}=\widehat{ADC}\)(1)
Xét (O) có
ΔADC nội tiếp đường tròn(A,D,C∈(O))
AD là đường kính(gt)
Do đó: ΔADC vuông tại C(Định lí)
Suy ra: \(\widehat{DAC}+\widehat{ADC}=90^0\)(Hai góc nhọn phụ nhau)(2)
Ta có: ΔABH vuông tại H(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(Hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{BAH}=\widehat{DAC}\)(đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp (O), H là trực tâm, AH cắt (O) tại E. Kẻ đường kính AOF. Chứng minh:
a) Tứ giác BCEF là hình thang cân
b) \(\widehat{BAE}=\widehat{CAF}\)
c) Gọi I là trung điểm của BC. Chứng minh: H, I, F thẳng hàng
a) Ta có B,C,F,E cùng thuộc đường tròn (O) => tứ giác BCEF nội tiếp
BCEF là hình thang cân
b) Ta có góc BAE = 90 độ - góc ABC = 90 độ - góc AFC = góc CAF
Suy ra: góc BAE = góc CAF
c) Ta có BH⊥AC
CF⊥AC
Suy ra BH//CF(1)
CH//BF(2)
Từ (1),(2)⇒tứ giác BHCF là hình bình hành
Mà I là trung điểm của BC
Suy ra I là trung điểm của HF hay I,H,F thẳng hàng
Đúng 2
Bình luận (0)
Câu 7. Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). có trực tâm là H.
a. Chứng minh rằng: BAH = OAC
b. Gọi M là trung điểm của BC. Chứng minh rằng: AH=2OM
Cho tam giác ABC nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC.AD là đường kính của (O). E thuộc AC sao cho HE//BC.1). Chứng minh rằng các đường thẳng BH và DE cắt nhau trên (O)2). Gọi F là giao điểm của các đường thẳng EH và AB. Chứng minh rằng A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF3). Gọi I là tâm đường tròn nội tiếp của tam giác DEF. Chứng minh rằng BE, CF và IH đồng quy.
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC.
AD là đường kính của (O). E thuộc AC sao cho HE//BC.
1). Chứng minh rằng các đường thẳng BH và DE cắt nhau trên (O)
2). Gọi F là giao điểm của các đường thẳng EH và AB. Chứng minh rằng A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Gọi I là tâm đường tròn nội tiếp của tam giác DEF. Chứng minh rằng BE, CF và IH đồng quy.
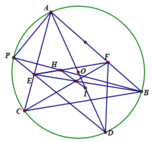
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
b) Dựng hình bình hành AHIO. Gọi J là tâm đường tròn ngoại tiếp tam giác OBC. Chứng minh rằng OI. OJ = R2
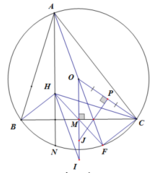
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm, I là tâm đường tròn nội tiếp tam giác.
a) Chứng minh rằng AI là tia phân giác của góc OAH.
b) Cho goc BAC = 60,, chứng minh rằng IO = IH
cho tam giác ABC có ba góc nhọn, trực tâm H. Người ta dựng hình bình hành BHCD và gọi I là giao điểm của 2 đường chéo.
a, CMR : tư giác ABDC nội tiếp được.
b, So sánh góc BAH và góc OAC (O là tâm đường tròn ngoại tiếp tam giác ABC)
c, Gọi G là giao điểm của AI và OH. CMR: G là trọng tâm tam giác ABC
Cho tam giác ABC nội tiếp đường tròn (O); gọi D là trung điểm của cạnh BC, H là trực tâm của tam giác ABC. Hai đường thẳng AD và OH cắt nhau tại G. Chứng minh rằng: G là trọng tâm của tam giác ABC.




















