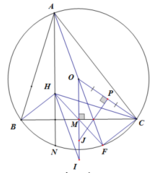
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AH = 2OM
Cho tam giác ABC nhọn, có H là trực tâm, nội tiếp đường tròn tâm O đường kính AM = 2R
a, Chứng minh tứ giác BHCM là hình bình hành
b, Gọi N là điểm đối xứng của M qua AB. Chứng minh tứ giác AHBN nội tiếp được trong một đường tròn
c, Gọi E là điểm đối xứng của M qua AC. Chứng minh ba điểm N, H, E thẳng hàng
d, Giả sử AB = R 3 . Tính diện tích phần chung của đường tròn (O) và đường tròn ngoại tiếp tứ giác AHBN
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Vẽ đường kính AK. gọi H là trực tâm , I là tâm đường tròn ngoại tiếp tam giác .
chứng minh rằng BHCK là hình bình hành
gọi m là trung điểm : chứng minh M H K thẳng hàng và AH= 2.OM
cho BAC = 60 độ, chứng minh rằng IO = IH
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), đường cao AD và trực tâm H. Gọi I là trung điểm của BC, AO cắt BC tại R. Qua R kẻ đường thẳng song song với IH cắt AH tại K. Gọi J là trung điểm của AH. Chứng minh rằng K là trực tâm của tam giác JBC
cho tam giác ABC nhọn nội tiếp đường tròn (o) có đường cao AN,CK .gọi H là trực tâm của tam giác ABC
đường tròn ngoại tiếp tam giác BNK cắt đường tròn (o) tại M (M khác B) Gọi E là trung điểm của đoạn thắng AC . Chứng minh E,M,H thẳng hàng
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
c) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH = ADK.
Cho tam giác ABC có 3 góc đều nhọn. Gọi O là tâm đường tròn ngoại tiếp, H là trực tâm, P là trung điểm cạnh AC của tam giác ABC.
a. Chứng minh BH= 2OP
b. Gọi L là trung điểm của BH, chứng minh LP bằng bán kính đường tròn ngoại tiếp tam giác ABC
Giúp với !! Hứa sẽ tick
Cho tam giác ABC vuông tại A. D là điểm thuộc BC. Có I,J là tâm đường tròn ngoại tiếp tam giác ADB và ADC. Gọi O là trung điểm của BC.
a/Chứng minh OI //AC
b/Chứng minh OJ vuông OI
c/ Chứng minh IJOD nội tiếp
