Question

Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC

c) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH = ADK.

Answer 1

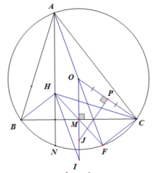
Ta có  NHC = ABC (cùng phụ với HCB)                         (1)

Vì ABDC là tứ giác nội tiếp nên ABC = ADC                  (2)

Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra

∆ADC = ∆AEC (c.c.c) => ADC = AEC                           (3)

Tương tự ta có AEK = ADK

Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180^o

Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)