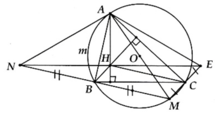
Cho tam giác ABC nhọn, có H là trực tâm, nội tiếp đường tròn tâm O đường kính AM = 2R
a, Chứng minh tứ giác BHCM là hình bình hành
b, Gọi N là điểm đối xứng của M qua AB. Chứng minh tứ giác AHBN nội tiếp được trong một đường tròn
c, Gọi E là điểm đối xứng của M qua AC. Chứng minh ba điểm N, H, E thẳng hàng
d, Giả sử AB = R 3 . Tính diện tích phần chung của đường tròn (O) và đường tròn ngoại tiếp tứ giác AHBN
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3












